次の図のような２つのコースがあります。太郎はＡコースを歩き、花子はＢコースを自転車で走ります。太郎と花子の速さの比は２：５です。２人はＣ地点を同時に同じ向きに出発します。太郎が１７周、花子が２５周すると２人は同時にＣ地点に戻ります。太郎が１周と５１４.８ｍ進んだとき、花子は２周してＣ地点にいました。
※ 画像はクリックすると拡大します。
(１) Ｂコース１周の長さはＡコース１周の長さの何倍ですか。
(２) Ｂコース１周の長さは何ｍですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
「速さの比」と「同じ時間に進む距離の比」は等しいので、太郎と花子が同じ時間に進む距離の比も２：５になります。
太郎がＡコースを１７周する時間で、花子はＢコースを２５周するので、Ａコース１７周とＢコース２５周の距離の比は２：５です。
また、比の内項と外項の積は等しいので、次の図の「Ａコース１７周×５」と「Ｂコース２５周×２」の答えは同じはずです。
※ 画像はすべて、クリックすると拡大します。
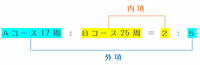
上の図の内項と外項の積をそれぞれ求めてみると、
・内項の積→Ａコース１７周×５＝Ａコース８５周
・外項の積→Ｂコース２５周×２＝Ｂコース５０周
となるので、Ａコース８５周とＢコース５０周の距離は等しいことが分かります。
つまり、Ａコース１周の長さ×８５＝Ｂコース１周の長さ×５０なので、ＡコースとＢコースの１周の長さの比は、Ａ：Ｂ＝５０：８５＝１０：１７です。
したがって、Ｂコース１周の長さは、Ａコース１周の長さの１７÷１０＝１.７倍になります。
(２)
太郎がＡコースを１周と５１４.８ｍ進む時間で、花子はＢコースを２周するので、「Ａコース１周＋５１４.８ｍ」と「Ｂコース２周」の長さの比は２：５になります。
また、さっきの問題で、Ａコース１周の長さを１０とおくと、Ｂコース１周の長さは１７と表せることが分かったので、
・Ａコース１周＋５１４.８ｍ→比の１０＋５１４.８ｍ
・Ｂコース２周→比の１７×２＝比の３４
と表せます。
つまり次の図のように、「比の１０＋５１４.８ｍ」と「比の３４」が２：５なので、さっきと同じように内項と外項の積をそれぞれ求めてみると、
・内項の積→(比の１０＋５１４.８ｍ)×５＝比の５０＋２５７４ｍ
・外項の積→比の３４×２＝比の６８
となります。
内項の積である「比の５０＋２５７４ｍ」と外項の積である「比の６８」を次のような２本の線分図にして比べてみると、比の６８－５０＝１８が２５７４ｍにあたることが分かります。
比の１は２５７４÷１８＝１４３ｍ、そしてＢコース１周の長さは比の１７なので、答えは１４３×１７＝２４３１ｍになります。
PR
