濃さが分からない食塩水が容器Ａに６００ｇ入っています。そこに３００ｇの水を加えてよく混ぜました。次に、食塩４０ｇだけが入っている容器Ｂに容器Ａから６００ｇだけ移してよく混ぜたところ、１０％の食塩水ができました。容器Ａに入っていた食塩水の濃さは何％ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずはこの問題で行った２段階の操作を図で確認しておきます。
【操作１】
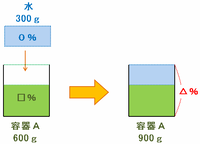
下の図のように、濃さ□％の食塩水が６００ｇ入っている容器Ａに水(濃さ０％の食塩水)を３００ｇ加えてうすめました。
このとき、容器Ａの中には濃さ△％の食塩水が６００＋３００＝９００ｇ入っています。
※ 画像はすべて、クリックすると拡大します。
【操作２】
濃さ△％の食塩水が９００ｇ入った容器Ａから６００ｇを取り出し、次の図のように食塩(濃さ１００％の食塩水)が４０ｇ入った容器Ｂにザバッと注いでよくかきまぜました。
このとき、食塩は「濃さ１００％の食塩水」と考えることができるので、天びん図を利用して容器Ａからやってきた食塩水の濃度を求めることができます。
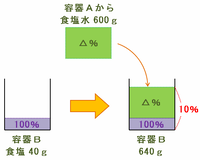
【容器Ａからきた食塩水６００ｇの濃度を求める天びん図】
上の操作２の図から、「容器Ａからきた濃度△％の食塩水６００ｇ」と「容器Ｂに入っていた食塩４０ｇ」を混ぜたら、濃さ１０％の食塩水ができたことが分かります。
したがって、その場面を天びん図に表してみると次の図のようになります。
容器Ａからきた食塩水とＢに入っていた食塩の重さの比はＡ：Ｂ＝６００ｇ：４０ｇ＝⑮：①なので、天びん図の左右のうでの長さの比は左：右＝①：⑮になります。
※ 重さの逆比は長さの比
上の図の赤い⑮が１００－１０＝９０％にあたるので、赤い①は９０÷⑮＝６％になります。
したがって、図の△％は１０－６＝４％になります。
【最初から容器Ａに入っていた食塩水の濃度を求める天びん図】
「最初から容器Ａに入っていた濃さ□％の食塩水６００ｇ」と「水３００ｇ」を混ぜてできた食塩水の濃さが４％であることが分かったので、その様子を天びん図に表してみると次の図のようになります。
上の図の赤い②が４－０＝４％にあたるので、赤い①は４÷②＝２％になります。
この問題で求めたいのは上の図の□％にあてはまる濃度なので、答えは４＋２＝６％になります。
PR
