Ａのビンには１２％の食塩水が４００ｇ、Ｂのビンには７％の食塩水が１６００ｇ入っています。今、この２つのビンから同じ量の食塩水を取り出し、Ａから取り出した食塩水をＢへ、Ｂから取り出した食塩水をＡへ入れてよくかき混ぜたら、Ａのビンに入っている食塩水は１１％の濃度になりました。
(１)
Ａのビンから取り出した食塩水の量は何ｇですか。
(２)
かき混ぜた後のＢのビンに入っている食塩水の濃度は何％ですか。考えた過程もかきなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
求めたいのは「Ａから取り出した食塩水の量」なのですが、ＡとＢからはそれぞれ同じ量の食塩水を取り出して交換したので、ＡとＢのどちらを求めても答えは同じはずです。
そこで、問題文にある「Ａのビンに入っている食塩水は１１％の濃度になりました」を天びん図に表して、Ｂから取り出してＡのビンに混ぜた食塩水の量を求めることにします。
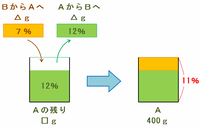
大まかに言うと、次の図のように「Ａのビンに残っている濃度１２％の食塩水□ｇ」と「Ｂから取り出してＡのビンに混ぜた濃度７％の食塩水△ｇ」を混ぜたら、濃度１１％の食塩水４００ｇができました。
※ 画像はすべて、クリックすると拡大します。
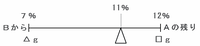
上の場面を天びん図に表すと、支点の左側にはＢから来た濃度７％で重さ△ｇの食塩水、支点の右側にはＡの残りである濃度１２％で重さ□ｇの食塩水、そして支点の上には２つを混ぜた後の濃度である１１％を次の図のように書き込みます。
このとき、上の図の支点よりも左側は１１－７＝４％、そして右側は１２－１１＝１％なので、うでの長さの比は左：右＝４：１になっています。
そして重さの比は長さの比の逆比なので、左：右＝１：４になります(次の図)。
つまり、混ぜた後の食塩水の重さの合計である４００ｇを支点の左右へ１：４の割合で比例配分してやれば、それぞれの重さが求められます。
支点の左側にある「ＢからＡへ移した食塩水の量」は４００×(５分の１)＝８０ｇ、ＡからＢへ移した食塩水の量もそれと同じなので、答えは８０ｇになります。
(２)
さっきの問題で「ＡからＢへ移した量」と「ＢからＡへ移した量」がそれぞれ８０ｇであることは確認しました。
次の図のように、Ｂのビンには濃度７％の食塩水が１６００－８０＝１５２０ｇ残っていて、そこにＡから濃度１２％の食塩水が８０ｇやってきます。
上の場面を天びん図に表してみると、左右の重さの比が１５２０ｇ：８０ｇ＝１９：１なので、うでの長さの比は次の図のように左：右＝１：１９になります。
上の図の１２－７＝５％が比の①＋⑲＝⑳にあたるので、比の①は５％÷⑳＝０.２５％になります。
以上から、上の図の□にあてはまる濃度(かき混ぜた後のＢ)は７＋０.２５＝７.２５％になります。
PR
