同じ濃さの食塩水をビーカーＡに１６０ｇ、ビーカーＢに２００ｇ入れました。２つのビーカーから同じ量の水を蒸発させたところ、ビーカーＡに残っている食塩水の濃さは１２％に、ビーカーＢに残っている食塩水の濃さは９％になりました。もとの食塩水の濃さは何％でしたか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
「食塩水を熱しても減るのは水だけで、食塩の重さは変化しない」ことを利用して問題を解いていきます。
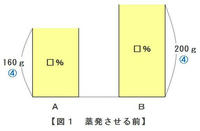
次の図１のように、水を蒸発させる前のビーカーＡとＢには、どちらも濃さ□％の食塩水が入っていました。
このとき、食塩水の重さの比はＡ：Ｂ＝１６０ｇ：２００ｇ＝４：５、そして２つの食塩水は濃度が等しいので、蒸発させる前のＡとＢに含まれる食塩の量の比も４：５になっているはずです。
※ 画像はすべて、クリックすると拡大します。
２つのビーカーから同じ量の水を蒸発させた後、Ａの食塩水の濃度は１２％、そしてＢの食塩水の濃度は９％になりました。
ただし、どちらのビーカーも蒸発して減ったのは水の量だけなので、食塩の量の比は蒸発させる前と同じくＡ：Ｂ＝４：５のままです。
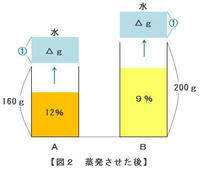
上の図で２つのビーカーから蒸発した水の量を[１]とおき、ＡとＢそれぞれのビーカーに残っている食塩水や食塩の量を式で表してみると・・・
・Ａの食塩水→１６０ｇ－[１]
・Ａの食塩→(１６０ｇ－[１])×０.１２＝１９.２ｇ－[０.１２]
・Ｂの食塩水→２００ｇ－[１]
・Ｂの食塩→(２００ｇ－[１])×０.０９＝１８ｇ－[０.０９]
となります。
食塩の量の比は４：５なので、Ａの食塩の量を５倍、Ｂの食塩の量を４倍すると２つの数は等しくなります。
そこで、さっそくその計算をして食塩の量をそろえてみると・・・
・Ａの食塩の５倍→(１９.２ｇ－[０.１２])×５＝９６ｇ－[０.６]
・Ｂの食塩の４倍→(１８ｇ－[０.０９])×４＝７２ｇ－[０.３６]
となります。
その２つの数を次のような２本の線分図に表して比べてみると、９６－７２＝２４ｇが、[０.６]－[０.３６]＝[０.２４]にあたることが分かります。
上の図の２４ｇが[０.２４]にあたるので、[１]にあたる量は２４ｇ÷[０.２４]＝１００ｇになります。
※ つまり、２つのビーカーから蒸発させた量はどちらも１００ｇ。
ビーカーＡから蒸発した水の量は１００ｇなので、蒸発した後に残った濃さ１２％の食塩水の量は１６０－１００＝６０ｇです。
このとき次の図のように、蒸発した水１００ｇをビーカーＡへ戻し、濃さ１２％の食塩水６０ｇと混ぜると、食塩水の濃さは蒸発させる前のときの濃度になります。
※ 時間を巻き戻して食塩水の濃度を元通りにする。
水は濃さ０％の食塩水として、水１００ｇと濃さ１２％の食塩水６０ｇを混ぜる様子を天びん図に表すと次のようになります。
上の図の重さの比は左：右＝１００ｇ：６０ｇ＝５：３なので、うでの長さの比は左：右＝３：５になります。
※ 重さの逆比は長さの比。
つまり、上の図の□％は１２％を３：５に比例配分した割合の３にあたるので、答えは１２×(８分の３)＝４.５％になります。
PR
