３５人の生徒が国語と算数のテストを受けました。どちらのテストも１０点満点で、得点は整数でつけています。７点以上とった生徒は、国語では１８人、算数では２５人でした。また、国語と算数の合計では、最高点が１８点で１人、最低点は８点で３人いました。次の問いに答えなさい。
(１)
国語、算数ともに７点以上とった生徒は、何人以上、何人以下いたと考えられますか。
(２)
国語、算数ともに７点以上とった生徒が１２人いたとき、国語と算数の合計点の平均は、最高で何点と考えられますか。四捨五入して小数第一位まで答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
国語、算数ともに７点以上とった生徒が最も少ない場合と多い場合の人数を、２つのベン図を利用してそれぞれ求めてみます。
【最も少ない場合のベン図】
両方の科目で７点以上取った人数が最も少なくなるのは、８点以下の３人もどちらかの科目で７点とったため、次のベン図でエが０人になるときです。
※ 画像はすべて、クリックすると拡大します。
その場合、上のベン図のアイウ＝３５人、アイ＝１８人、イウ＝２５人なので、イにあてはまる人数は１８＋２５－３５＝８人になります。
【最も多い場合のベン図】
両方の科目で７点以上取った人数が最も多くなるのは、国語で７点以上とった人はすべて算数でも７点以上だったため、次のベン図のように国語の輪が算数の輪の中へ完全に入ったときです。
その場合、両方の科目で７点以上とった人数(上のベン図のイ)は国語で７点以上とった人数と等しいので１８人になります。
以上から、両方の科目で７点以上とった人数は、最も少ない場合で８人、最も多い場合は１８人になります。
(２)
次のベン図のイが１２人なので、アは１８－１２＝６人、ウは２５－１２＝１３人、そしてエは３５－(６＋１２＋１３)＝４人であることが分かります。
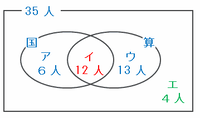
アの６人は国語だけが７点以上なので、最も合計点が高くなるのは「国語が１０点、算数が６点」の場合です。
イの１２のうち１人は合計が最高の１８点であることが分かっているので、残りの１１人の合計点は最も高くて１７点であることが分かります。
ウの１３人は算数だけが７点以上なので、最も合計点が高くなるのは「国語が６点、算数が１０点」の場合です。
エの４人のうち３人は合計が最低の８点であることが分かっています。また、残り１人の合計点はどちらの科目も７点未満であることから、最も高くて「国語が６点、算数も６点」の１２点になります。
以上のことをふまえてア～エそれぞれの合計得点を求めてみると、
・ア→(１０＋６)×６＝９６点
・イ→１８＋１７×１１＝２０５点
・ウ→(６＋１０)×１３＝２０８点
・エ→８×３＋１２＝３６点
となることから、３５人全員の合計点は最も高くて９６＋２０５＋２０８＋３６＝５４５点になることが分かります。
したがって、そのときの平均点は５４５÷３５＝１５.５７…＝１５.６点になります。
PR
