容器Ａには５％の食塩水が１００ｇ、容器Ｂには３％の食塩水が１５０ｇ、容器Ｃには２.５％の食塩水が１００ｇ入っています。今、よくかき混ぜてＡから３０ｇを取り出してＢに入れました。次に、よくかき混ぜてＢから何ｇかを取り出してＣに入れました。さらに、よくかき混ぜてＣから( )ｇを取り出してＡに入れたところ、Ａ、Ｂ、Ｃの３つの容器に含まれる食塩の重さが等しくなりました。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずはそれぞれの容器に含まれている食塩の量を求めてみると、
・容器Ａ→１００×０.０５＝５ｇ
・容器Ｂ→１５０×０.０３＝４.５ｇ
・容器Ｃ→１００×０.０２５＝２.５ｇ
となるので、３つの容器に含まれる食塩の合計は５＋４.５＋２.５＝１２ｇになります。
また、この問題では３つの容器の間で食塩水をやり取りするだけなので、やり取りを終えた後も食塩の合計は１２ｇのままです。
したがって、やり取りを終えた後の３つの容器には、食塩がそれぞれ１２÷３＝４ｇずつ含まれていることが分かります。
【やり取り① ＡからＢへ食塩水を３０ｇ移す】
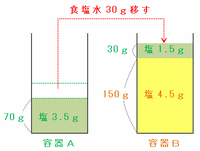
容器Ａの食塩水３０ｇの中には、食塩が３０×０.０５＝１.５ｇ含まれているので、次の図のように容器ＡからＢへ食塩水を３０ｇ移すと、
・容器Ｂの食塩の量→４.５＋１.５＝６ｇ
・容器Ｂの食塩水の量→１５０＋３０＝１８０ｇ
となります。
また、やり取りを終えた後の容器Ａには濃さ５％の食塩水が１００－３０＝７０ｇ残っているので、その中には食塩が７０×０.０５＝３.５ｇ含まれています。
※ 画像はすべて、クリックすると拡大します。
【やり取り② ＢからＣへ食塩水を何ｇか移す】
さっきのやり取りで容器Ｂに含まれる食塩の量は６ｇになったので、その量を４ｇに減らすためには、次のやり取りでＣへ食塩を６－４＝２ｇ移せばＯＫです。
２÷６＝３分の１なので、次の図のように容器ＢからＣへ食塩水を１８０×３分の１＝６０ｇ移せば、ＢからＣへ食塩が２ｇ移動します。
また、このやり取りを終えた後、容器Ｃには食塩水が１００＋６０＝１６０ｇ、そして食塩が２.５＋２＝４.５ｇ含まれています。
【やり取り③ ＣからＡへ食塩水を何ｇか移す】
さっきのやり取りで容器Ｃに含まれる食塩の量は４.５ｇになったので、その量を４ｇに減らすためには、次のやり取りでＡへ食塩を４.５－４＝０.５ｇ移せばＯＫです。
０.５÷４.５＝９分の１なので、次の図のように容器Ｃに入っている食塩水の９分の１をＡへ移せば、ＣからＡへ食
塩が０.５ｇ移動します。
上の図の容器Ｃには食塩水が１６０ｇ入っているので、Ａへ移す食塩水の量は１６０×９分の１＝９分の１６０ｇになります。
※ 最後のやり取りの後、容器Ａに含まれる食塩の量は３.５＋０.５＝４ｇになったので、これで３つの容器に含まれる食塩の量がすべて４ｇでそろいました。
PR
