５をいくつか並べた整数をＡとします。そのＡに５をかけた整数の各位の数の和をＢとするとき、次の問いに答えなさい。
(１)
整数Ａが５を３５個並べた数のとき、Ｂを求めなさい。
(２)
Ｂ＝６８６のとき、Ａは５をいくつ並べた数ですか。５の個数を求めなさい。
(３)
Ｂの各位の数の和を求めると９になりました。このようなＢのうち、３番目に小さい数を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
実際に５を３５個並べた数に５をかけて、その答えの各位の数の和を求めてもＯＫですが、それだと紙の横幅が足りなくて大変そうなので、まずは５を２個、３個、４個、・・・と並べた場合で規則性を調べてみます。
Ａ＝５５のときは、５５×５＝２７５となりますが、次の図のようにいちばん上の位にある２といちばん下の位にある５を足すと、ちょうど７が１個できるので、２＋７＋５＝７×２＝１４となります。
※ 画像はすべて、クリックすると拡大します。
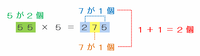
Ａ＝５５５のときは、５５５×５＝２７７５となりますが、次の図のようにいちばん上の位にある２といちばん下の位にある５を足すと、さっきと同じように７が１個できるので、２＋７＋７＋５＝７×３＝２１となります。
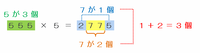
Ａ＝５５５５のときは、５５５５×５＝２７７７５となりますが、次の図のようにいちばん上の位にある２といちばん下の位にある５を足すと、やはり７が１個できるので、２＋７＋７＋７＋５＝７×４＝２８となります。
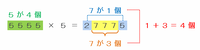
ここまでに確認したことをまとめてみると、
・Ａに５を２個並べたとき→Ｂは７が２個あると考えればＯＫ
・Ａに５を３個並べたとき→Ｂは７が３個あると考えればＯＫ
・Ａに５を４個並べたとき→Ｂは７が４個あると考えればＯＫ
となっているので、Ａに５を□個並べたとき、Ｂは７が□個あると考えられることが分かります。
つまりＡに５を３５個並べた場合も、Ｂは次の図のように「７が３５個ある」と考えればＯＫなので、答えは７×３５＝２４５になります。
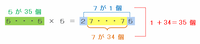
(２)
６８６÷７＝９８なので、Ｂには７が９８個並んでいると考えられます。
また、さっきの問題で「Ａに並んでいる５の個数とＢに並んでいる７の個数は等しい」と考えられることが分かったので、Ａにも５が９８個並んでいます。
(３)
Ｂの各位の数の和は「７×□」を計算すれば求められるので、答えは必ず７の倍数になっているはずです。
また、９×２＝１８、９×３＝２７、９×４＝３６などの例を見れば分かるように、各位の数の和が９になるのは９の倍数のときなので、答えは必ず９の倍数にもなっているはずです。
つまり、Ｂの各位の数の和が９になるのは「７の倍数」かつ「９の倍数」のときなので、７と９の公倍数を小さい順に調べてみると、
・最小公倍数の６３→６＋３＝９なのでＯＫ
・６３×２＝１２６→１＋２＋６＝９なのでＯＫ
・６３×３＝１８９→１＋８＋９＝１８なのでダメ
・６３×４＝２５２→２＋５＋２＝９なのでＯＫ
となることから、３番目に小さい数は２５２になります。
※ Ｂに７が２５２÷７＝３６個分並んだとき。つまりＡにも５が３６個並んでいる。
【補足】
解説の中で「各位の数の和が９になるのは９の倍数のとき」と書きましたが、厳密にいえば「各位の数の和が９の倍数ならば、その数自体も９の倍数である」が正しい表現です。
つまり、各位の数の和が９のときはもちろん、９×２＝１８とか９×３＝２７になった場合でも、その数は９の倍数です。
・３１５→３＋１＋５＝９なので、３１５は９の倍数。
・６５４３→６＋５＋４＋３＝１８なので、６５４３は９の倍数。
・５９２３８→５＋９＋２＋３＋８＝２７なので、５９２３８は９の倍数。
PR
