気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
09/06
Mon
2010
頌栄女子2010【6】 ☆濃度・食塩水のやり取り☆
A、Bの容器にそれぞれ500gずつの食塩水が入っています。次の各問いに答えなさい。なお、答えの求め方も説明しなさい。
(1)
AからBに200g移してよくかき混ぜ、次にBからAに200g移しました。Aは最初5%の食塩水でしたが、7%になりました。Bは最初何%の食塩水でしたか。
(2)
(1)の後、Aから何gかをBに移し、同じ量をAにもどしたとき、Aは7.5%の食塩水になりました。何g移しましたか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
(1)
まずは図を使って、AとBの間でどのようなやり取りが行われたのかを確認してみます。
※ 画像はすべて、クリックすると拡大します。
【図1 最初の状態】
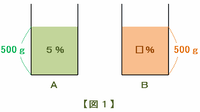
最初は容器Aに濃さ7%の食塩水が500g、容器Bには濃さ□%の食塩水が500g入っています。
この問題で求めたいのはこの□%にあてはまる濃度です。
※ 画像はすべて、クリックすると拡大します。
※ 画像はすべて、クリックすると拡大します。
【図2 AからBへ食塩水を移す】
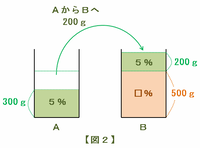
まずは図2のように容器Aから食塩水を200g取り出し、それを容器Bへと移します。
このとき、容器Aには5%の食塩水が500-200=300g残り、容器Bの食塩水は200+500=700gになります。
【図3 容器Bの食塩水の濃度が変わった】
【図3 容器Bの食塩水の濃度が変わった】
容器Aから来た濃さ5%の食塩水200gと、もともと容器Bに入っていた食塩水500gをクルクルとかき混ぜた結果、容器Bの食塩水の濃度は□%から△%へと変化しました。
とはいっても、それが果たして濃くなったのか薄くなったのかも今のところは分かっていません。

【図4 BからAへ食塩水を移す】
【図4 BからAへ食塩水を移す】
今度は容器Bから濃さ△%の食塩水200gを容器Aへ移します。
このとき、容器Bには濃さ△%の食塩水が700-200=500g残り、容器Aは食塩水の量が300+200=500gになります。

【図5 容器Aの濃さが変わった】
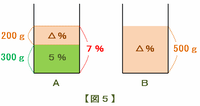
【図5 容器Aの濃さが変わった】
下の図の容器Aでは、もともとAに残っていた濃さ5%の食塩水300gと、Bから来た濃さ△gの食塩水200gが混ざった結果、濃さ7%の食塩水ができました。
ここまでの流れを振り返ってみると、「図2→図3」と「図4→図5」のときに食塩水の濃度が変わっているので、それぞれの場面を天びん図で表して□%や△%にあてはまる数を求めてみます。
【その1 △%にあてはまる数を求める】
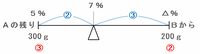
さっきの図4から図5への流れを天びん図に表すと、支点の左側にはAに残っていた濃度7%・重さ300gの食塩水、右側にはBから来た濃度△%・重さ200gの食塩水、そして支点の上には2つを混ぜた後の濃度である7%を次のように書き込みます。
このとき、左右の重さの比は左:右=300g:200g=3:2なので、うでの長さの比は左:右=2:3になります。
※ 重さの逆比は長さの比。
つまり、上の図の7-5=2%が青い比の②にあたるので、比の①は1%、そして比の③は3%になります。
上の図の△%は7%から右へ3%進んだ地点にあるので、7+3=10%になります。
【その2 □%にあてはまる数を求める】
さっきの天びん図で求めた10%は、図2から図3で「容器Aから来た濃さ5%・重さ200gの食塩水」と「容器Bに入っていた濃さ□%・重さ500gの食塩水」を混ぜたときの濃度です。
そのときの様子を天びん図に表すと、次の図のようになります。
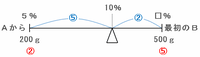
上の図の重さの比は左:右=200g:500g=2:5なので、長さの比は左:右=5:2になります。
青い比の⑤が10-5=5%にあたるので、比の①は1%、そして比の②は2%です。
図の□%は10%から右へ2%進んだ地点にあるので、答えは10+2=12%になります。
(2)
この問題はいきなり天びん図を使おうとするとむしろややこしくなるので、途中までは「食塩水全体×濃度=食塩水の量」という公式をうまく利用して問題を解いてみます。
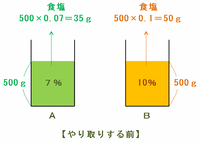
容器AとBとの間で食塩水をやり取りする前は、次の図のようにAには濃さ7%の食塩水が500g、Bには濃さ10%の食塩水が500g入っています。
このとき、それぞれの容器に含まれる食塩の量を求めてみると・・・
・容器A→500×0.07=35g
・容器B→500×0.1=50g
となっています。
次に容器AとBとの間で食塩水をやり取りした後の状態を確認しておくと、下の図のようにAには濃さ7.5%の食塩水が500g、Bには濃さ□%の食塩水が500g入っています。
このとき、容器Aに含まれる食塩の量は500×0.075=37.5gとなり、やり取りする前より37.5-35=2.5g増えました。
※ したがって、Bの食塩水はAより濃いことが分かります。
また、容器Bに含まれる食塩の量はさっきよりも2.5g減ったはずなので、50-2.5=47.5gになります。
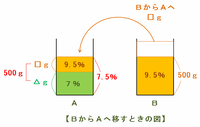
つまり、容器AとBとの間で食塩水をやり取りした後のBは、食塩水500gの中に食塩が47.5gふくまれていることが分かるので、その濃度は47.5÷500×100=9.5%になります。
この図を見れば分かるように、容器Aでは「もともとAに入っていた濃さ7%・重さ△gの食塩水」と「Bから来た濃さ9.5%・重さ□gの食塩水」が混ざった結果、濃さ7.5%の食塩水ができました。
ここでAとBとの間で行われたやり取りの流れを振り返っておくと・・・
① 容器AからBへ濃さ7%の食塩水を□g移してよくかき混ぜた
② 容器Bの食塩水の濃度は9.5%になった
③ 容器BからAへ濃さ9.5%の食塩水を□g移してよくかき混ぜた
④ 容器Aの食塩水の濃度は7.5%になった
という感じです。
この図を見れば分かるように、容器Aでは「もともとAに入っていた濃さ7%・重さ△gの食塩水」と「Bから来た濃さ9.5%・重さ□gの食塩水」が混ざった結果、濃さ7.5%の食塩水ができました。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
