１辺の長さが６㎝の立方体があります。その立方体の各面に、図１の正四角すいを図２のようにはりつけます。(図２は、２つの面に対してだけはりつけてあります)
このとき、２つの正四角すいの頂点Ａ、Ｂを通る直線と立方体の辺ＣＤが交わりました。
※ 画像はすべて、クリックすると拡大します。
立方体の６つのすべての面に図１の正四角すいをはりつけて新しい立方体アを完成させるとき、次の各問いに答えなさい。
(１)
立体アは図２の四角形ＡＣＢＤと同じ形の四角形から作られます。立体アには、この四角形がいくつありますか。
(２)
立体アの体積を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、正四角すいの側面にはＡＢＣ、ＡＣＤ、ＡＤＥ、ＡＢＥの４つの三角形があります。
※ 画像はすべて、クリックすると拡大します。
立方体は全部で６面あるので、すべての面に正四角すいをはりつけたとき、立体の表面には三角形が全部で４×６＝２４個あります。
下の図のように、ＡＣＢＤと同じ四角形を１つ作るためには三角形が２つずつ必要なので、立体アには全部で２４÷２＝１２個の四角形ができます。
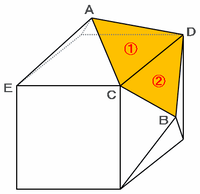
(２)
立方体に正四角すいを２個くっつけた図を、次のように正面から見てみると、頂点ＡとＢを結んだ赤い直線は立方体の頂点Ｃを通過しています。
このとき、下の図の角ＥＣＦは直角なので、角ＡＣＥと角ＢＣＦの大きさはどちらも(１８０－９０)÷２＝４５度になります。
今度は次の図のように、正四角すいの頂点Ａから真下に向けてピシッと直線を引くと、三角形ＡＣＧができます。
下の図の角ＡＣＧは４５度、角ＡＧＣは９０度、そして角ＣＡＧは１８０－(４５＋９０)＝４５度なので、ＡＣＧは直角二等辺三角形になっていることが分かります。
このとき、下の図の辺ＧＣの長さは６÷２＝３㎝なので、正四角すいの高さにあたる辺ＡＧの長さも３㎝になります。
立方体の体積は６×６×６＝２１６㎤、正四角すい１個の体積は６×６×３÷３＝３６㎤なので、立方体に正四角すい６個をはりつけてできる立体アの体積は、２１６＋３６×６＝４３２㎤になります。
PR
