Ａの容器に１２％の食塩水が４００ｇ、Ｂの容器に８％の食塩水が５００ｇ入っています。今、ＢからＡに何ｇか移したところ、Ａに含まれている食塩の量がＢに含まれている食塩の量の３倍になりました。次の問いに答えなさい。
(１) 初めにＡ、Ｂの容器に含まれていた食塩はそれぞれ何ｇですか。
(２) ＢからＡに移した食塩水は何ｇですか。
(３) ＢからＡに移した後のＡの食塩水の濃度は何％になりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
Ａの容器に含まれる食塩の量は食塩水全体の１２％なので、答えは４００×０.１２＝４８ｇになります。
また、Ｂの容器に含まれる食塩の量は食塩水全体の８％なので、答えは５００×０.０８＝４０ｇです。
※ どちらも次の問題を解くのに必要な数字です。
(２)
２つの容器に含まれる食塩の量の合計は４８＋４０＝８８ｇなので、Ａに含まれている食塩の量がＢに含まれている食塩の量の３倍になったときの関係を線分図に表すと次のようになります。
※ 画像はすべて、クリックすると拡大します。
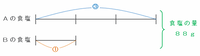
上の図の３＋１＝４めもりが８８ｇにあたるので、食塩水をＡに移した後の容器Ｂに残っている食塩の量は、８８÷４＝２２ｇになります。
また、ＢからＡへ移した食塩水の中には、４０－２２＝１８ｇの食塩が含まれていたことも分かるので、容器Ｂの中の食塩水は次の図のように表すことができます。
上の図のように、容器Ａへ移ったこさ８％の食塩水□ｇのうち、食塩の量は１８ｇなので、Ａへ移った食塩水の量は１８÷０.０８＝２２５ｇになります。
(３)
次のように、「Ｂから移ったこさ８％の食塩水２２５ｇ」と「Ａに入っていたこさ１２％の食塩水４００ｇ」を混ぜる天びん図を利用して答えを求めます。
上の図の重さの比は左：右＝２２５ｇ：４００ｇ＝９：１６なので、長さの比は左：右＝１６：９になります。
※ 重さの逆比は長さの比
つまり、上の図の１２－８＝４％が青い比の１６＋９＝２５にあたるので、青い比の１は４÷２５＝０.１６％になります。
求めたいのは８％から右へ青い比の１６だけ進んだ地点のこさ(図の赤い□％)なので、答えは８＋０.１６×１６＝１０.５６％になります。
PR
