次の立体は、一部が欠けた直方体の上にななめに切った円柱をのせた形をしています。図１はこの立体を正面から見た図、図２は真上から見た図で、欠けた部分の曲線は円の４分の１です。この立体の体積を求めなさい。ただし、円周率は３.１４とします。
※ 画像はすべて、クリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
大まかに言うと、まずは下段と上段の体積を別々に求め、それらを合体して答えを求めればＯＫです。
ただし、円周率を使う問題はなるべく「×３.１４」を後回しにすることに気をつけながら解いていきます。
【下段の体積を求める】
下段の立体は、次の図のように「たて８㎝、横８㎝、高さ５㎝の直方体」から「半径４㎝、高さ５㎝の円柱の４分の１」を切り取った形になっています。
※ 画像はすべて、クリックすると拡大します。
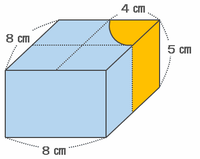
上の図の直方体の体積は８×８×５＝３２０㎤、そしてオレンジ色の部分の体積は４×４×３.１４×５÷４＝２０×３.１４㎤と表せます。
【上段の体積を求める】
次の２つの投影図から、上段にある立体は底面が直径４㎝(半径２㎝)で、左辺の高さが１１－５＝６㎝、右辺の高さが４㎝の円柱っぽい形であることが分かります。
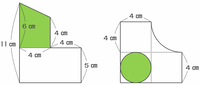
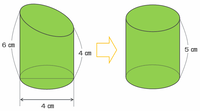
左右の高さが違うままだと体積が求められないので、次の図のように高さが(６＋４)÷２＝５㎝の円柱として体積を求めてみると、２×２×３.１４×５＝２０×３.１４㎤になります。
※ 左右の高さの平均をとり、それと同じ高さの円柱の体積を求める。
【上段と下段の体積を合体する】
上段の体積は２０×３.１４㎤、そして下段の体積は３２０㎤から２０×３.１４㎤を引いたものなので、立体すべての体積を求める式は(２０×３.１４㎤)＋３２０㎤－(２０×３.１４㎤)と表せます。
このとき、「２０×３.１４㎤」は式から消去できるので、答えは３２０㎤になります。
【補足】
底面の半径が２倍で高さが等しい円柱の体積は２×２＝４倍、その４分の１は４÷４＝１倍です。
つまり、「底面の半径２㎝の円柱」と「底面の半径４㎝の円柱の４分の１」は計算するまでもなく体積が同じ(高さが等しい場合)なので、それを切り取って上にくっつけても体積は最初(直方体のとき)と変わりません。
という発想ができれば、円周率を使うまでもなく「８×８×５＝３２０㎤」でおしまいです。
PR
