次の図１のように、Ｐ町からＱ町までの間に２つの峠があります。Ａ君はＰ町からＱ町へ、Ｂ君はＱ町からＰ町へ向かって同時に出発して歩いて行きました。２人の歩く速さは等しく、上りは毎時２㎞、下りは毎時４㎞で一定です。２人のかかった時間とＰ町からの道のりとの関係を図２で示しています。
※ 画像はすべて、クリックすると拡大します。
(１) Ｐ町からＱ町までの道のりは何㎞ですか。
(２) 峠から峠までの道のりは何㎞ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、Ａ君はＰ町からアイウエの順に進んでＱ町まで５.１時間かかり、Ｂ君はＱ町からオカキクの順に進んでＰ町まで４.８時間かかりました。
つまり、上りを毎時２㎞、下りを毎時４㎞の速さでＰ町とＱ町との間を往復すると、５.１＋４.８＝９.９時間かかることが分かります。
※ 画像はすべて、クリックすると拡大します。
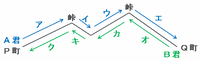
２人とも上りは毎時２㎞、下りは毎時４㎞で進むので、速さの比は上り：下り＝毎時２㎞：毎時４㎞＝１：２、そして時間の比は上り：下り＝２：１になります。
つまり、ＰＱ間を次の図のアキウオ(すべて上り)とクイカエ(すべて下り)で進んだ場合の時間の比はアキウオ：クイカエ＝２：１なので、アキウオにかかる時間は９.９×(３分の２)＝６.６時間、クイカエにかかる時間は９.９×(３分の１)＝３.３時間になります。
※ 往復(アイウエ＋オカキク)にかかる９.９時間を２：１に比例配分しています。
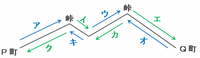
つまり、ＰＱ間は上りの速さである毎時２㎞で進めば６.６時間、下りの速さである毎時４㎞で進めば３.３時間かかるので、その距離は２×６.６＝１３.２㎞、または４×３.３＝１３.２㎞となります。
(２)
Ｐ町を出発したＡ君は、１３.２㎞離れたＱ町まで５.１時間かけて進みました。
また、そのときに進んだ道のりは次の図のように上り(ア＋ウ)と下り(イ＋エ)の２種類に分けられるので、まずはつるかめ算を利用して、上り(ア＋ウ)の距離を求めてみます。
もしＡ君が下りの速さである毎時４㎞で５.１時間進み続けると、４×５.１＝２０.４㎞進みます。
しかし実際のＰＱ間は１３.２㎞なので、つるかめ算の公式を利用して毎時２㎞で進んだ時間を求めると、(２０.４－１３.２)÷(４－２)＝３.６時間になります。
したがって、上の図のアとウの距離の合計は２×３.６＝７.２㎞だと分かります。
ここからは説明の都合上、次の図のようにＰＱ間にある峠や谷を左から順にＲ、Ｓ、Ｔとおいて話を進めます。
２人の進み方を表したグラフにＰからＱまでの点を書き込んでみると次のようになります。
このグラフを見ると、Ａ君はＰからＳまで２.４時間かかり、Ｂ君はＳからＰまで４.８－３＝１.８時間かかっていることが分かります。
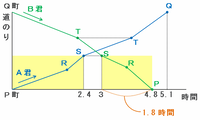
つまり、上りを毎時２㎞、下りを毎時４㎞で次の図のアイキクの順にＰＳ間を往復すると、２.４＋１.８＝４.２時間かかります。
その４.２時間は、上り(ア＋キ)と下り(イ＋ク)で２：１に比例配分することができるので、ＰＳ間を上りの速さで進むと４.２×(３分の２)＝２.８時間、下りの速さで進むと４.２×(３分の１)＝１.４時間かかります。
したがって、上の図のＰＳ間の距離は２×２.８＝５.６㎞(または４×１.４＝５.６㎞)であることが分かります。
ここまでの流れから、Ｐ町を出発したＡ君は次の図のアとイのように進み、５.６㎞離れたＳ地点に到着するまでに２.４時間かかったことが分かりました。
上りと下りの２種類が混ざっていて、合計の距離も時間も分かっているので、ここからはつるかめ算を利用してアの距離を求めてみます。
もしＡ君が２.４時間ずっと下りの速さである毎時４㎞で進むと、その距離は４×２.４＝９.６㎞になります。
しかし実際の距離は５.６㎞なので、つるかめ算の公式を利用して上りの速さである毎時２㎞で進んだ時間を求めると、(９.６－５.６)÷(４－２)＝２時間になります。
したがって、上りであるＰＲ間の距離は２×２＝４㎞、そして下りであるＲＳ間の距離は５.６－４＝１.６㎞になります。
以上から、次の図のアは４㎞、イは１.６㎞、そしてウは７.２－４＝３.２㎞となるので、峠と峠の間の距離(図のＲＳ＋ＳＴ)は１.６＋３.２＝４.８㎞になります。
【補足】
この問題のように上りと下りが混ざっている場合は、
① 上りと下りの速さの比を求める
② 逆比にして時間の比に直す
③ 往復にかかる時間を比例配分して上りまたは下りにかかる時間を求める
④ 「上りの速さ×上りにかかる時間」または「下りの速さ×下りにかかる時間」
という流れで距離を求めることができます。
また、２つの速さが混ざっていて、距離と時間の合計が分かっていればつるかめ算を利用することができます。
PR
