次の図のように、同じ大きさの立方体を３６個積み上げ固定して直方体を作ります。ただし、すべての面が黒い立方体が１１個、すべての面が白い立方体が２５個です。このとき、次の各問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
図の状態で、すべての面が見えていない立方体の個数は何個ですか。
(２)
アの方向から見ると白の立方体だけが見え、イの方向から見ると黒の立方体は４個だけ見えるとします。図の状態で、すべての面が見えていない立方体の見え方は何通りありますか。
(３)
立方体を積み上げたまま、上の面が下の面になるように、直線Ｌを軸として矢印の方向に直方体を１８０度回転させます。回転させる前と後で、黒の立方体があった位置に黒の立方体が移動したのが２組４個であるとします。図の状態で、すべての面が見えていない立方体の入れ方は何通りありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図を利用して見えている立方体の数を確認してみると、
① 真上から・・・青い○を付けた１２個が見える
② 真正面から・・・緑色の○を付けた６個が見える(青い○をつけたものは除く)
③ 右から・・・オレンジ色の○を付けた６個が見える(青と緑の○をつけたものは除く)
となることから、見えている立方体の合計は１２＋６＋６＝２４個になります。
※ 画像はすべて、クリックすると拡大します。
(２)
黒い立方体は全部で１１個あるのですが、次の図だと９個までしか確認できないので、残りの２個は見えない１２個の中に使われています。
また、アの方向からは白の立方体しか見えないので、真後ろにある９個はすべて白であることも分かります。
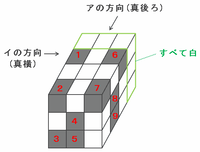
【いちばん左側にある列の模様について】
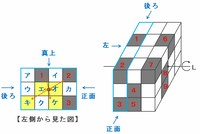
次の図の青い枠で囲まれた部分は、直方体の中でいちばん左側にある列を表しています。
この直方体を左側から見ると黒い立方体が４個あるはずなので、次の図のア～エのどこか１か所に黒い立方体をあてはめます。
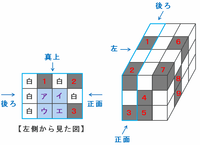
【中央にある列の模様について】
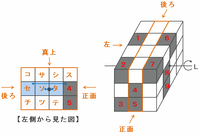
次の図のオレンジ色の枠で囲まれた部分は、直方体の中央にある列を表しています。
黒い立方体の残り２個のうち、１個はさっきの図のア～エのどこかで使うので、もう１つは次の図のオ～クのどこかにあてはめればＯＫです。
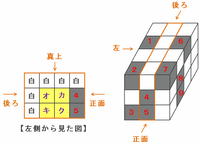
つまり、まだ場所が決まっていない黒い立方体２個のあてはめ方は、
・いちばん左側にある列→ア～エのうちどこか１か所にあてはめるので４通り
・中央にある列→オ～クのうちどこか１か所にあてはめるので４通り
となることから、その組み合わせは全部で４×４＝１６通りになります。
(３)
直方体を１回転させる前後で同じ位置に黒い立方体が来るためには、次のいちばん右側にある列の図の「６」と「９」のように、黒い立方体が回転軸と点対称の位置にあればＯＫです。
※ つまり、２組４個のうちの１組は右側面にある「６」と「９」です。
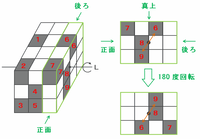
残りの１組はいちばん左の列、または中央の列にあるはずなので、「見えていない部分に黒い立方体があと２個隠れているよー」ということを頭の片隅に置きながら、その組み合わせを探してみます。
【いちばん左側にある列の模様について】
次の図の青い枠で囲まれた部分は、直方体の中でいちばん左側にある列を表しています。
この左側の面に回転させる前後で同じ位置に黒い立方体が来る場所の候補を探してみると、下の図のア～ケについて次のようなことが分かります。
・アとイとカ→もともと白い立方体であることが分かっている。
・ウ→カが白色なので、ウを黒色にして一回転させても黒色にはならない。
・エとオ→両方とも黒色であれば、回転する前後でどちらも黒色になる。
・キ→２が黒色なので、キを黒色にすれば回転する前後でどちらも黒色になる。
・ク→イが白色なので、クを黒色にして一回転させても黒色にはならない。
・ケ→１が黒色なので、ケを黒色にすれば回転する前後でどちらも黒色になる。
したがって、回転させる前後で同じ位置に黒い立方体が来る組をいちばん左側の面に１つ作るためには、
・エとオを両方黒色にする→黒い立方体は２個しか残っていないので、他の場所はすべて白。
・キまたはケのどちらかを黒色にする→黒い立方体の残り１個は中央の列で使う。
ことが分かります。
******補足********************************************
残り２個の黒い立方体をキとケにあてはめてしまうと、回転させる前後で同じ位置に黒い立方体が来る組が３つになってしまう(右側面に１組、左側面に２組)ので、問題文の条件にあてはまりません。
******補足終わり**************************************
【中央にある列の模様について】
次の図のオレンジ色の枠で囲まれた部分は、直方体の中央にある列を表しています。
この面に回転させる前後で同じ位置に黒い立方体が来る場所の候補を探してみると、下の図のコ～テについて次のようなことが分かります。
・コとサとシとス→もともと白い立方体であることが分かっている。
・セ→４が黒色なので、セを黒色にすれば回転する前後でどちらも黒色になる。
・ソとタ→両方とも黒色であれば、回転する前後でどちらも黒色になる。
・チ→スが白色なので、チを黒色にして一回転させても黒色にはならない。
・ツ→シが白色なので、ツを黒色にして一回転させても黒色にはならない。
・テ→サが白色なので、テを黒色にして一回転させても黒色にはならない。
したがって、回転させる前後で同じ位置に黒い立方体が来る組を中央の面に１つ作るためには、
・ソとタを両方黒色にする→黒い立方体は２個しか残っていないので、他の場所はすべて白。
・セを黒色にする→黒い立方体の残り１個はいちばん左側の列で使う。
ことが分かります。
今までの流れをまとめると、次の図の「エとオ」、「ソとタ」のどちらの組み合わせで黒い立方体を２個使えば、残りはすべて白色になります。
また、「キ」と「ケ」と「セ」のどれかひとつを黒色にした場合、黒い立方体の残り１個はそれ以外の場所へあてはめることになります。
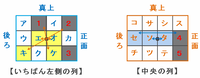
例えば「エとオ」や「ソとタ」に黒い立方体を２個使った場合、他の場所はすべて白色になるので、
・「エとオ」は黒→他の場所はすべて白
・「ソとタ」は黒→他の場所はすべて白
という色の使い方しかありません。
したがって、「エとオ」または「ソとタ」に黒い立方体を２個使う場合の色の使い方は、全部で１＋１＝２通りになります。
一方、例えば「キ」に黒い立方体を使った場合、もう１個の黒い立方体は上の図の「ウ・エ・オ・ク・ソ・タ・チ・ツ・テ」の９か所のうちどこか１か所にあてはめるので、色の使い方は９通りになります。
******補足***********************************************************
「キ」に黒い立方体を使った場合、回転させても黒色のままになる２組目が「２とキ」で完成したので、残り１個の黒い立方体を「ケ」や「セ」にあてはめて３組目を作った時点でアウトです。
また、「ア・イ・カ・コ・サ・シ・ス」はもともと白い立方体であることが分かっているので、黒色にすることはできません。
******補足終わり*****************************************************
「ケ」や「セ」に黒い立方体を１個あてはめた場合も同じように９通りずつできるので、「キ」と「ケ」と「セ」のどれかひとつを黒色にする場合の色の使い方は、全部で９×３＝２７通りになります。
以上から、答えは２＋２７＝２９通りになります。
PR
