次の図のように、底面の半径が６ｍ、高さが８ｍの円すいの中に球Ｓ、Ｔがあります。球Ｓは円すいに側面と底面で接しており、球Ｔは円すいの側面と球Ｓに接しています。
※ 画像はクリックすると拡大します。
(１) 円すいと球Ｓが接する所には円ができます。この円の周りの長さは何㎝ですか。
(２) 球Ｔの半径は何ｍですか。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
この円すいの頂点Ａから底面に向かって垂線を引き、次の図のように真正面から見ると、左右２つの三角形に分かれます。
このとき、右側にできた三角形ＡＤＣは、３辺の長さの比がＤＣ：ＡＤ：ＡＣ＝３：４：５の直角三角形になっています。
※ 画像はすべて、クリックすると拡大します。
次に球Ｓと円すいの側面にできる線をＥＦとすると、下の図の三角形ＡＧＦは三角形ＡＤＣと相似なので、ＧＦ：ＡＧ：ＡＦも３：４：５になっています。
今度は球Ｓの中心である点Ｈから辺ＡＣへ垂線を引いてみると、三角形ＡＦＨは三角形ＡＤＣと相似になるので、ＦＨ：ＡＦ：ＡＨも３：４：５になっています。
このとき、辺ＡＦは上の比だと⑤、下の比だと④になっているので、この比を最小公倍数である⑳にそろえます。
そのとき、次の図のように上の比は全体を４倍、下の比は全体を５倍することになります。
このそろえた比を円すいの図に書き込んでみると次のようになるのですが、辺ＤＨも辺ＦＨと同じく球Ｓの半径なので、長さは⑮と表すことができます。
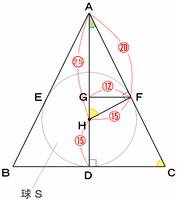
このとき、円すいの高さである８ｍは比の２５＋１５＝４０にあたるので、比の１は８÷４０＝０.２ｍになります。
また、辺ＧＦの長さは比の１２なので、０.２×１２＝２.４ｍです。
辺ＧＦは求める円の半径にあたるので、円の周りの長さは２.４×２×３.１４＝１５.０７２ｍになります。
(２)
次の図のように、２つの球の境目に辺ＩＪを引くと、三角形ＡＫＪと三角形ＡＤＣは相似になります。
また、辺ＤＨと辺ＫＨはどちらも球Ｓの半径なので比の１５、辺ＫＤは１５×２＝３０、辺ＡＤは比の４０なので、辺ＡＫの長さは比の４０－３０＝１０と表せます。
つまり、三角形ＡＤＣと三角形ＡＫＪの相似比は、辺ＡＤ：辺ＡＫ＝４０：１０＝４：１になっています。
このとき、次の図のように三角形ＡＤＣと三角形ＡＫＪを並べてみると、この２つの三角形は対応する辺の比がすべて４：１なので、右の図の辺ＬＭ(球Ｔの半径)の長さは左の図の辺ＦＨの４分の１になっているはずです。
辺ＦＨの長さは比の１５なので、辺ＬＭの長さは比の１５÷４＝３.７５にあたることが分かります。
比の１は０.２ｍなので、辺ＬＭの長さ(つまり球Ｔの半径)は０.２×３.７５＝０.７５ｍになります。
PR
