次の図のように、時計の文字盤の一部に色を付けました。このとき、次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
１日(２４時間)の中で、長針と短針の両方が色のついた部分に入っている時間は、何時間何分ですか。
(２)
１日(２４時間)の中で、長針と短針の両方またはどちらか一方が色のついた部分に入っている時間は、何時間何分ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは午前中の１２時間の中で条件にあてはまる時間を探し、その答えを２倍して答えを求めます。
【両方の針が同じ場所にいる場合】
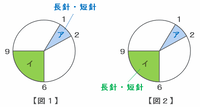
長針と短針の両方が次の図１のアにいるのは、１時５分から１時１０分までの５分間です。
また、図２のように両方の針がイにいるのは、「６時３０分から６時４５分まで」、「７時３０分から７時４５分まで」、「８時３０分から８時４５分まで」のそれぞれ１５分ずつになります。
※ 画像はクリックすると拡大します。
したがって、両方の針が同じ場所にいる時間の合計は５＋１５×３＝５０分になります。
【どちらかの針がア、もうひとつの針がイにいる場合】
次の図３や図４のように、「短針→ア・長針→イ」あるいは「短針→イ・長針→ア」という位置関係の場合でも、両方の針が色のついた部分に入っていることになります。
図３のように「短針→ア・長針→イ」となるのは、１時３０分から１時４５分までの１５分間です。
また、図４のように「短針→イ・長針→ア」となるのは、「６時５分から６時１０分まで」、「７時５分から７時１０分まで」、「８時５分から８時１０分まで」のそれぞれ５分ずつです。
したがって、どちらかの針がア、もうひとつの針がイにいる時間の合計は１５＋５×３＝３０分になります。
以上から、両方の針が色のついた部分にいる時間は５０＋３０＝８０分となるのですが、それは午前中の１２時間に限った話なので、１日(２４時間)の場合は８０×２＝１６０分＝２時間４０分になります。
(２)
この問題で求めたい時間を、次のベン図を使って確認してみると・・・
・図のＡ→長針だけが色のついた部分を通過する時間
・図のＢ→長針と短針の両方が色のついた部分を通過する時間(２時間４０分)
・図のＣ→短針だけが色のついた部分を通過する時間
・図のＤ→どちらの針も色のついた部分を通っていない時間
となるので、この問題で求めたい「長針と短針の両方またはどちらか一方が色のついた部分に入っている時間」は、下の図のＡＢＣにあたります。
上の図のＢが２時間４０分であることはさっきの問題で求めたので、あとはＡとＣをそれぞれ求めればＡＢＣの合計が分かるのですが、実はＤを求めてＡＢＣＤ(２４時間)から引く方がスムーズに答えを求められます。
１時間の中で長針が次の図５のウ・エ・オを通過するのは、「０分から５分まで」と「１０分から３０分まで」と「４５分から６０分まで」の合わせて５＋２０＋１５＝４０分間です。
また、午前中の１２時間のうち、短針が次の図５のウ・エ・オを通過するのは、「０時から１時まで」と「２時から６時まで」と「９時から１２時まで」の合わせて８時間です。
したがって、午前中の１２時間のうち、長針と短針のどちらもアとイを通過しない時間の合計は、４０×８＝３２０分＝５時間２０分になります。
つまり、１日(２４時間)の中で長針と短針のどちらもアとイを通過しない時間の合計は５時間２０分×２＝１０時間４０分になります。
※ さっきのベン図のＤが１０時間４０分
求めたいのはさっきのベン図のＡＢＣにあたる時間なので、答えは２４時間－１０時間４０分＝１３時間２０分になります。
PR
