次の図１のような正三角形を積み重ねます。図２は２段積み重ねた状態、図３は３段積み重ねた状態です。
※ 画像はすべて、クリックすると拡大します。
図２の２段の状態のとき、正三角形の数は４個(△が３個と▽が１個)、頂点の数は６個、辺の数は９本と数えるものとします。
３段以上積み重ねたときも正三角形の数、頂点の数、辺の数を同じように数えます。次の問いに答えなさい。
(１)
５段積み重ねたときの正三角形の数、頂点の数、辺の数はそれぞれいくつですか。
(２)
正三角形の数が２８９になるのは、正三角形を何段積み重ねたときですか。
(３)
頂点の数が１０５になるのは、正三角形を何段積み重ねたときですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは正三角形を１段、２段、３段積み重ねたときの図を使って、正三角形の数、頂点の数、辺の数などがどのように増えていくのかを確かめてみます。
【正三角形の数の増え方】
次の図を見れば分かるように、正三角形の数は１段のときは１個、２段のときは１＋３＝４個、３段のときは１＋３＋５＝９個、・・・という感じで増えていきます。
このとき、正三角形を□段積んだときの正三角形の数は、１から□までの奇数の和になっていることが分かります。
※ 画像はすべて、クリックすると拡大します。
【頂点の数の増え方】
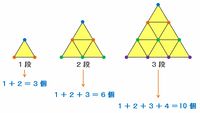
次の図を見れば分かるように、頂点の数は１段のときは１＋２＝３個、２段のときは１＋２＋３＝６個、３段のときは１＋２＋３＋４＝１０個、・・・という感じで増えていきます。
このとき、正三角形を□段積んだときの頂点の数は、１から□＋１までの整数の和になっていることが分かります。
【辺の数の増え方】
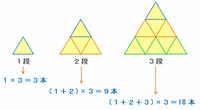
次の図を見れば分かるように、辺の数は１段のときは１×３＝３本、２段のときは(１＋２)×３＝９本、３段のときは(１＋２＋３)×３＝１８本、・・・という感じで増えていきます。
このとき、正三角形を□段積んだときの辺の数は、(１から□までの数の和)×３で求められることが分かります。
以上から、正三角形を５段積み重ねたときの正三角形の数は１＋３＋５＋７＋９＝２５個、頂点の数は１＋２＋３＋４＋５＋６＝２１個、そして辺の数は(１＋２＋３＋４＋５)×３＝４５本になります。
(２)
正三角形を□段まで積み重ねたときの正三角形の数は、１から□までの奇数の和を計算すれば求められるので、１からどんどん奇数を足していって２８９になるときを見つけても答えは求められます。
しかし次の図を見れば分かるように、１から□までの奇数の和は□×□を計算すれば求められるので、同じ数をかけ合わせて２８９になるときを探してみると、１７×１７のときであることが分かります。
以上から、正三角形の数が２８９個になるのは１７段積み重ねたときになります。
(３)
正三角形を□段積んだときの頂点の数は、１から□＋１までの整数の和を計算すれば求められるので、その合計が１０５になるときを地道に求めてみます。
１から１０までの整数の和は(１＋１０)×１０÷２＝５５なので、さらにそこから整数を加えていくと、次の図のように１４まで足したときであることが分かります。
以上から、頂点の数が１０５個になるのは正三角形を１４段積み重ねたときになります。
PR
