１０を０より大きい３つの整数に分ける分け方は、(１・１・８) 、(１・２・７) 、(１・３・６) 、(１・４・５) 、(２・２・６) 、(２・３・５) 、(２・４・４) 、(３・３・４)の８通りあります。２０を０より大きい３つの整数に分ける分け方は( )通りあります。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
問題文を読むと、どの組み合わせもカッコの中は３つの数が左から小さい順に並んでいることが分かります。
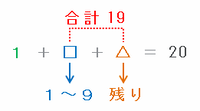
そこで、次の図のようにいちばん左の数を１、真ん中の数を□、そして右側の数を△とおき、「１＋□＋△」の合計が２０になる場合(ただし１≦□≦△とする)を考えてみると、
・□と△の和は２０－１＝１９
・左端の数が１なので、□には１以上の数があてはまる
・１９÷２＝９余り１なので、□には９以下の数があてはまる
・△には２０から１と□にあてはめた数を引いた残りがあてはまる
となることから、合計が２０となる(１・□・△)の組み合わせは、□に１から９のいずれかをあてはめた場合の９通りであることが分かります。
※ 画像はすべて、クリックすると拡大します。
次の図のように、いちばん左の数が２と３の場合もそれぞれ何通りできるか考えてみると、
・左端が２なら、□と△の和は２０－２＝１８
・１８÷２＝９なので、□には２以上９以下の数があてはまる
・左端が３なら、□と△の和は２０－３＝１７
・１７÷２＝８余り１なので、□には３以上８以下の数があてはまる
となることから、(２・□・△)の組み合わせは□に２から９のいずれかをあてはめた場合の８通り、(３・□・△)の組み合わせは□に３から８のいずれかをあてはめた場合の６通りとなります。
次の図のように、いちばん左の数が４と５の場合は、
・左端が４なら、□と△の和は２０－４＝１６
・１６÷２＝８なので、□には４以上８以下の数があてはまる
・左端が５なら、□と△の和は２０－５＝１５
・１５÷２＝７余り１なので、□には５以上７以下の数があてはまる
となることから、(４・□・△)の組み合わせは□に４から８のいずれかをあてはめた場合の５通り、(５・□・△)の組み合わせは□に５から７のいずれかをあてはめた場合の３通りです。
次の図のように、いちばん左の数が６と７の場合は、
・左端が６なら、□と△の和は２０－６＝１４
・１４÷２＝７なので、□には６または７のどちらかがあてはまる
・左端が７なら、□と△の和は２０－７＝１３
・１３÷２＝６余り１となるが、□は左端の数である７以上でなければダメ
となることから、(６・□・△)の組み合わせは□に６または７のどちらかをあてはめた場合の２通り、そして(７・□・△)の組み合わせは□が６以下になってしまうため作れないことが分かります。
以上から、合計が２０となる３つの数の組み合わせは、全部で９＋８＋６＋５＋３＋２＝３３通りになります。
PR
