次の図１のように、円周の６等分点に１から６までの番号がついています。６等分点のうち、さいころを投げて最初に出た目の数の番号の点から始めて、さいころを投げて出た目の数の番号の点を順に結んで折れ線を作ります。折れ線全体が１つの三角形の周になるとき、「折れ線は１つの三角形になる」と呼ぶことにします。
※ 画像はすべて、クリックすると拡大します。
たとえば、出た目が順に２、３、４、４、２のとき、折れ線は１つの三角形になります(図２)。この例のように、同じ目が続いたときは、次に異なる目が出るまで折れ線はその番号の点でとどまることとします。また、２、３、４、２、４のときも、折れ線は１つの三角形になります(同じく図２)。この例のように、一度結んだ線をもう一度結ぶときも、その線は１本の線であるとします。
２、４、６、４、６のとき、１、４、６、２、１のとき、１、３、５、１、２のときは、それぞれ図３、図４、図５のようになり、折れ線は１つの三角形になりません。
さいころを４回投げるとき、折れ線が１つの三角形になるような目の出方は( ① )通り、さいころを５回投げるとき、折れ線が１つの三角形になるような目の出方は( ② )通りです。ただし、さいころの目の出る順序も区別するものとします。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
①
４回サイコロを振ったときに折れ線が１つの三角形になるためには、次の図のように
・ ６個の点から好きな１個を選ぶ(点Ａ)。
・ 残った５個の点からどれか１つを選ぶ(点Ｂ)。ついでにＡとＢを直線で結ぶ。
・ 残った４個の点からどれか１つを選ぶ(点Ｃ)。ついでにＢとＣを直線で結ぶ。
・ 点Ａと同じ目を出して、ＣとＡを直線で結ぶ。
という流れでサイコロの目が出ればＯＫです。
※ 画像はすべて、クリックすると拡大します。
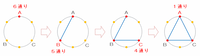
上の図の点Ａ(１回目)の選び方は１から６の６通り、点Ｂ(２回目)の選び方はＡ以外の目ならＯＫなので５通り、そして点Ｃ(３回目)の選び方はＡとＢ以外の目ならＯＫなので４通りあります。
また、最後は必ずＣからＡに戻らなければならないので、４回目のサイコロの目は１回目と同じ数しかあり得ません。
※ つまり、４回目のサイコロの目の出方は１通り。
以上から、サイコロを４回振ったときに折れ線が１つの三角形になるような目の出方は、６×５×４×１＝１２０通りになります。
②
さっきの問題で、４回のサイコロの目が「Ａ→Ｂ→Ｃ→Ａ」の順になれば、折れ線が１つの三角形になることが分かりました。
つまりサイコロを５回振る場合も、３つの点のどこかで１回途中下車して「Ａ→Ａ→Ｂ→Ｃ→Ａ」、「Ａ→Ｂ→Ｂ→Ｃ→Ａ」、「Ａ→Ｂ→Ｃ→Ｃ→Ａ」のように進めば、３つの点を「Ａ→Ｂ→Ｃ」の順に選び、最後にＣとＡを結んで三角形を作ることができます(次の図参照)。
また、次の図のように４回目のサイコロまでは「Ａ→Ｂ→Ｃ→Ａ」の順に進み、５回目のサイコロでＡ、Ｂ、Ｃのどれかの目が出れば、やはり三角形を作ることができます(次の図参照)。
次の図のようにサイコロの目が「Ａ→Ｂ→Ａ→Ｃ→Ｂ」となった場合も、３つの点が「Ａ→Ｂ→Ｃ」の順に選ばれ、最後にＣとＢが結ばれて三角形が完成します。
※ 指でなぞってみると右回りに見えても、３つの点を選ぶ順番はこれまでの６パターンと同じく左回り。
これまでに出てきた７通りの図は、どれもサイコロの目の出方が「６通り・５通り・４通り」と「１通り・１通り」の組み合わせになっているので、答えは６×５×４×１×１×７＝８４０通りになります。
PR
