次の図で、点Ａから点Ｂまで一筆書きする方法は、何通りありますか。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずは一筆書きする図形全体を次の図のように赤い点線の上と下に分け、進み方がそれぞれ何通りあるのかを確認してみます。
※ 画像はすべて、クリックすると拡大します。
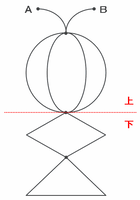
【赤い点線よりも上の部分の進み方】
一筆書きを完成させるためには、次の図のＡからＣへ進んだ線がアイウエの４本の曲線を進んだ後、再びＣに戻っている必要があります。
※ 「ＡからＣ」→「アイウエ」→「ＣからＢ」という流れで一筆書きが完成する。
上の図の曲線アイウエをすべて通り終えたときにＣにいるためには、４本の曲線をＣから出発して「下向き→上向き→下向き→上向き」の順に進めばＯＫです。
このとき、４本の曲線の通り方を数えてみると・・・
・１本目(下向き)→４本のうちのどれか１本を選ぶので４通り
・２本目(上向き)→３本のうちのどれか１本を選ぶので３通り
・３本目(下向き)→２本のうちのどちらかを選ぶので２通り
・４本目(上向き)→最後に残った１本を選ぶので１通り
となることから、４本の曲線の通り方は全部で４×３×２×１＝２４通りになります。
【赤い点線よりも下の部分の進み方】
次の図のように、赤い点線よりも下の部分には「ひし形」と「三角形」がひとつずつあります。
たとえばひし形の部分の進み方を考えてみると、
・ＤからＥへ進むには、左の道か右の道のどちらか１つを選ぶので２通り
・ＥからＤへ戻るには、さっき選ばなかった道を進めばいいので１通り
となることから、全部で２×１＝２通りになります。
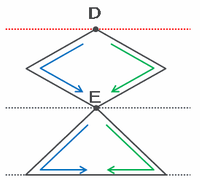
また、最下部の三角形の部分の進み方は、左回りか右回りでＥに戻ってくるしかないので２通りと考えます。
したがって、赤い点線よりも下の部分の進み方は全部で２×２＝４通りになります。
ここまでの流れをまとめてみると、下の図のようにＣＤ間の進み方は２４通り、そしてＤより下の進み方は４通りなので、一筆書きの方法は全部で２４×４＝９６通りになります。
おしまい。
と言いたいところなのですが、この問題の場合はもうひとつだけ考えるべきポイントがあります。
【その１ 曲線を１本通った後にＤより下へ進む場合】
たとえば次の図のように、まずはＡからＣへ進んだ後、
① 曲線を１本通ってＤへ進み
② Ｄより下のひし形と三角形を通って再びＤに戻り
③ 曲線の残り３本を通ってＣに進む
という流れの後にＢへ行く方法があります。
【その２ 曲線を３本通った後にＤより下へ進む場合】
たとえば次の図のように、まずはＡからＣへ進んだ後、
① 曲線を３本通ってＤへ進み
② Ｄより下のひし形と三角形を通って再びＤに戻り
③ 曲線の残り１本を通ってＣに進む
という流れの後にＢへ行く方法があります。
つまり、ＣとＤの間の進み方が２４通り、Ｄより下の進み方が４通り、そしてＤより下に進むタイミングが２通りあるので、一筆書きの方法は全部で２４×４×２＝１９２通りになります。
PR
