電卓の数字のように、０から９までの数字を次の図のように表します。この数字を使って、上下をさかさまにしても同じ数に見える数を作ります。例えば、２けたの数なら１１や６９などです。このような３けたの数は全部で何個ありますか。同じ数字を何回選んでもかまいません。
※ 画像はすべて、クリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
次の図の５個の数字「０」、「１」、「２」、「５」、「８」は、上下をさかさまにしても元の数字と同じになります。
※ 画像はすべて、クリックすると拡大します。
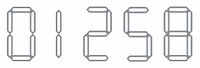
また、次の図の「６」を上下さかさまにすると「９」に、そして「９」を上下さかさまにすると「６」に変わります。
【６と９を使わない場合】
次の図のように、３けたの数「ＡＢＣ」のＡとＣには「１・１」、「２・２」、「５・５」、「８・８」の組み合わせの中からどれか１つを選んであてはめ、Ｂには「０・１・２・５・８」の中からどれか１つを選んで入れると、上下さかさまにしてもすべての位の数が同じままになります。
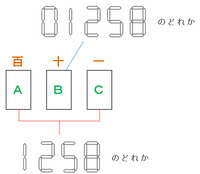
その場合、ＡとＣの数のあてはめ方が４通り、Ｂの数のあてはめ方が５通りなので、３けたの数は全部で４×５＝２０通りできます。
【６と９を使う場合】
「６」と「９」を次の図のＢで使うと、上下さかさまにしたときに「６」は「９」へ、「９」は「６」へと変わってしまうのでアウトです。
そこで下の図のように、ＡとＣの組み合わせを「６と９」または「９と６」にしてあてはめ、残ったＢには「０・１・２・５・８」の中からどれか１つを選んで使います。
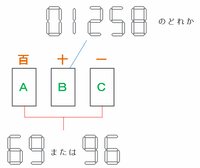
この場合、ＡとＣのあてはめ方は２通り、Ｂのあてはめ方は５通りなので、３けたの数の作り方は全部で２×５＝１０通りになります。
つまり、「６」と「９」を使わない場合は３けたの数が２０個、使う場合は１０個作れるので、答えは全部で２０＋１０＝３０個になります。
【補足】
某四谷大塚の過去問速報サイトだと、答えが「３４個」になってました。
・百の位と一の位が同じパターン→４×５＝２０通り
・百の位と一の位を「６・９」または「９・６」にする→２×５＝１０通り
・３つの位がすべて同じ数→「１１１・２２２・５５５・８８８」の４通り
したがって、答えは全部で２０＋１０＋４＝３４通り、とのことです。
んーと、百の位と一の位が同じパターンを「４×５」と計算する場合、
・百の位と一の位の組み合わせは「１・１」、「２・２」、「５・５」、「８・８」の４通り
・十の位は「０・１・２・５・８」のどれか１つだから５通り
と考えてると思うので、その中に「１１１」とか「２２２」みたいなのも含まれてるんじゃないかと・・・
あれ？もしかしてなんかすごい勘違いしてますか？そういうのって、案外自分だと気がつかないんですよね(汗)
PR
