次の図のように、Ｏを中心とする面積が１２㎠の円板があり、その周を１２等分する位置に点Ａ、Ｂ、Ｃ、・・・、Ｌがあります。これらの周上の点から２点を選んで、次のように円板を２つの図形に分けます。たとえばＡとＣを選んだとき、ＯＡとＯＣで切ります。このときできる２つの図形の面積はそれぞれ２㎠、１０㎠です。
※ 画像はすべて、クリックすると拡大します。
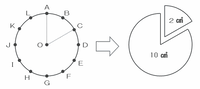
今、Ａ、○、□の３つの点から２点を選んで上と同じ操作をします(○、□はＢ、Ｃ、Ｄ、・・・、Ｌの１１個の点のうちのどれか)。たとえば○がＢ、□がＥのとき、できる図形の面積として考えられるのは１㎠、３㎠、４㎠、８㎠、９㎠、１１㎠の６通りです。次の問いに答えなさい。
(１)
○がＣ、□がＦのとき、できる図形の面積として考えられるものをすべて答えなさい。
(２)
次のア～エのそれぞれの場合について、考えられる○と□の組をすべて答えなさい。答えは(ＣＦ)のように書きなさい。(ＦＣ)と(ＣＦ)は同じなので、どちらか一方を答えなさい。
ア できる図形が２通り
イ できる図形が３通り
ウ できる図形が４通り
エ できる図形が５通り
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
３点Ａ、Ｃ、Ｆから２つの点を選んだときの組み合わせは(ＡＣ)、(ＡＦ)、(ＣＦ)の３通りです。
たとえば次の図のように(ＡＣ)を選んで円板を切断した場合、青い２㎠のおうぎ形ができ、残りの黄色い部分は１２－２＝１０㎠のおうぎ形になります。
※ 画像はすべて、クリックすると拡大します。
次の図のように(ＡＦ)を選んで円板を切断した場合、青い５㎠のおうぎ形ができ、残りの黄色い部分は１２－５＝７㎠のおうぎ形になります。
また、(ＣＦ)を選んで円板を切断した場合、青い３㎠のおうぎ形ができ、残りの黄色い部分は１２－３＝９㎠のおうぎ形になります。
以上から、できる図形の面積として考えられるものを小さい順に並べると「２㎠、３㎠、５㎠、７㎠、９㎠、１０㎠」となります。
【補足】
大まかに言うと、
・３つの点から２つを選ぶ組み合わせは３通り
・円板を切断したときにできる面積は「小さい方」と「大きい方」の２通り
なので、できる面積は最大で３×２＝６通りになります。
(２)のア
３つの点から２つを選ぶ組み合わせが３通りであることは変えようがないので、できる図形の面積を２通りまで減らすためには、３通りの切断の仕方でできた「小さい図形」と「大きい図形」の面積を、それぞれ同じにする必要があります。
※ たとえば、どの切断の仕方でも「小さい図形」の面積は５㎠、「大きい図形」の面積は７㎠みたいな感じ。
次の図のように、円の中心から３点Ａ、Ｅ、Ｉへ向けて線を引くと、円板はア～ウの３か所に等分されます。
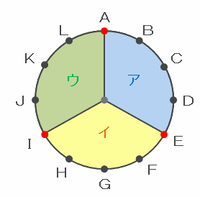
上の図のア～ウの面積はどれも１２÷３＝４㎠なので、３点Ａ、Ｅ、Ｉから
・ＡＥを選んで切断→ア(４㎠)とイウ(８㎠)に分かれる
・ＡＩを選んで切断→ウ(４㎠)とアイ(８㎠)に分かれる
・ＥＩを選んで切断→イ(４㎠)とアウ(８㎠)に分かれる
となることから、円板の面積は４㎠と８㎠の２種類しかできません。
円板の面積を３等分する分け方は上の図のパターンしかないので、答えは(ＥＩ)だけです。
(２)のイ
できる図形の面積を３通りにするには、３つの点から２つを選ぶ組み合わせである３通りが、
・１通り目→「小さい図形」と「大きい図形」の面積が異なる
・２通り目→「小さい図形」と「大きい図形」の面積が、どちらも１通り目と同じ
・３通り目→「小さい図形」と「大きい図形」の面積が同じ(つまり、円板を半分に切断)
のようになればＯＫです。
次の図のように、円の中心から３点Ａ、Ｄ、Ｇへ向けて線を引くと、円板はア～ウの３か所に分かれます。
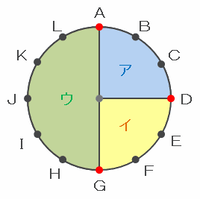
上の図のアとイはどちらも円板の４分の１にあたる３㎠、ウは円板の半分にあたる６㎠なので、３点Ａ、Ｄ、Ｇから
・ＡＤを選んで切断→ア(３㎠)とイウ(９㎠)に分かれる
・ＡＧを選んで切断→ウ(６㎠)とアイ(６㎠)に分かれる
・ＤＧを選んで切断→イ(３㎠)とアウ(９㎠)に分かれる
となることから、円板の面積は３㎠、６㎠、９㎠の３種類できます。
また、次の図のように３点を「ＡＤＪ」や「ＡＧＪ」の組み合わせにしても、さっきの図と条件が変わらないので、答えは(ＤＧ)、(ＤＪ)、(ＧＪ)の３通りになります。
(２)のウ
できる図形の面積を４通りにするには、３つの点から２つを選ぶ組み合わせである３通りが、
・１通り目→「小さい図形」と「大きい図形」の面積が異なる
・２通り目→「小さい図形」と「大きい図形」の面積が、どちらも１通り目と異なる
・３通り目→「小さい図形」と「大きい図形」の面積が、どちらも１通り目または２通り目と同じ
のようになればＯＫです。
【パターンその１】
次の図のように、円の中心から３点Ａ、Ｂ、Ｃへ向けて線を引くと、円板はア～ウの３か所に分かれます。
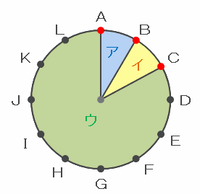
上の図のアとイはどちらも円板の１２分の１にあたる１㎠、ウは円板の６分の５にあたる１０㎠なので、３点Ａ、Ｂ、Ｃから
・ＡＢを選んで切断→ア(１㎠)とイウ(１１㎠)に分かれる
・ＡＣを選んで切断→ウ(１０㎠)とアイ(２㎠)に分かれる
・ＢＣを選んで切断→イ(１㎠)とアウ(１１㎠)に分かれる
となることから、円板の面積は１㎠、２㎠、１０㎠、１１㎠の４種類できます。
また、上の図と同じ条件にできる３点の組み合わせとしては、他にもＡＢＬ、ＡＫＬがあります。
【パターンその２】
次の図のように、円の中心から３点Ａ、Ｃ、Ｅへ向けて線を引くと、円板はア～ウの３か所に分かれます。
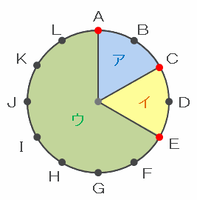
上の図のアとイはどちらも円板の６分の１にあたる２㎠、ウは円板の３分の２にあたる８㎠なので、３点Ａ、Ｃ、Ｅから
・ＡＣを選んで切断→ア(２㎠)とイウ(１０㎠)に分かれる
・ＡＥを選んで切断→ウ(８㎠)とアイ(４㎠)に分かれる
・ＣＥを選んで切断→イ(２㎠)とアウ(１０㎠)に分かれる
となることから、円板の面積は２㎠、４㎠、８㎠、１０㎠の４種類できます。
また、上の図と同じ条件にできる３点の組み合わせとしては、他にもＡＣＫ、ＡＩＫがあります。
【パターンその３】
次の図のように、円の中心から３点Ａ、Ｆ、Ｋへ向けて線を引くと、円板はア～ウの３か所に分かれます。
上の図のアとイはどちらも円板の１２分の５にあたる５㎠、ウは円板の６分の１にあたる２㎠なので、３点Ａ、Ｆ、Ｋから
・ＡＦを選んで切断→ア(５㎠)とイウ(７㎠)に分かれる
・ＡＫを選んで切断→ウ(２㎠)とアイ(１０㎠)に分かれる
・ＦＫを選んで切断→イ(５㎠)とアウ(７㎠)に分かれる
となることから、円板の面積は２㎠、５㎠、７㎠、１０㎠の４種類できます。
また、上の図と同じ条件にできる３点の組み合わせとしては、他にもＡＦＨ、ＡＣＨがあります。
パターン１から３までに出てきた３点の組み合わせから、答えは(ＢＣ)、(ＢＬ)、(ＫＬ)、(ＣＥ)、(ＣＫ)、(ＩＫ)、(ＦＫ)、(ＦＨ)、(ＣＨ)の９通りになります。
(２)のエ
できる図形の面積を５通りにするには、３つの点から２つを選ぶ組み合わせである３通りが、
・１通り目→「小さい図形」と「大きい図形」の面積が異なる
・２通り目→「小さい図形」と「大きい図形」の面積が、どちらも１通り目と異なる
・３通り目→「小さい図形」と「大きい図形」の面積が同じ(つまり、円板を半分に切断)
のようになればＯＫです。
【パターンその１】
次の図のように、円の中心から３点Ａ、Ｂ、Ｇへ向けて線を引くと、円板はア～ウの３か所に分かれます。
上の図のアは円板の１２分の１にあたる１㎠、イは円板の１２分の５にあたる５㎠、ウは円板の２分の１にあたる６㎠なので、３点Ａ、Ｂ、Ｇから
・ＡＢを選んで切断→ア(１㎠)とイウ(１１㎠)に分かれる
・ＡＧを選んで切断→ウとアイはどちらも６㎠になる
・ＢＧを選んで切断→イ(５㎠)とアウ(７㎠)に分かれる
となることから、円板の面積は１㎠、５㎠、６㎠、７㎠、１１㎠の５種類できます。
また、上の図と同じ条件にできる３点の組み合わせとしては、他にもＡＦＧ、ＡＧＨ、ＡＧＬ、ＡＢＨ、ＡＦＬがあります。
【パターンその２】
次の図のように、円の中心から３点Ａ、Ｃ、Ｇへ向けて線を引くと、円板はア～ウの３か所に分かれます。
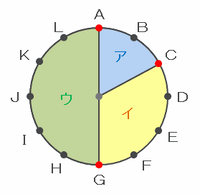
上の図のアは円板の６分の１にあたる２㎠、イは円板の３分の１にあたる４㎠、ウは円板の２分の１にあたる６㎠なので、３点Ａ、Ｃ、Ｇから
・ＡＣを選んで切断→ア(２㎠)とイウ(１０㎠)に分かれる
・ＡＧを選んで切断→ウとアイはどちらも６㎠になる
・ＣＧを選んで切断→イ(４㎠)とアウ(８㎠)に分かれる
となることから、円板の面積は２㎠、４㎠、６㎠、８㎠、１０㎠の５種類できます。
また、上の図と同じ条件にできる３点の組み合わせとしては、他にもＡＥＧ、ＡＧＩ、ＡＧＫ、ＡＣＩ、ＡＥＫがあります。
パターン１と２に出てきた３点の組み合わせから、答えは(ＢＧ)、(ＦＧ)、(ＧＨ)、(ＧＬ)、(ＢＨ)、(ＦＬ)、(ＣＧ)、(ＥＧ)、(ＧＩ) 、(ＧＫ)、(ＣＩ)、(ＥＫ)の１２通りになります。
PR
