Ａ、Ｂ、Ｃの３人が、ある池の周囲に沿った道を歩きます。Ａが２周するのにかかる時間はＢが３周するのにかかる時間と等しく、Ｂが１周するのにかかる時間に２０分加えるとＣが２周するのにかかる時間と等しくなります。また、３人がそれぞれ１周するのにかかる時間の合計は１時間３４分です。
(１)
Ｃがこの道を歩いて池を１周するのに何分かかりますか。
(２)
３人の歩く速さの比を求めなさい。
(３)
この道のＰ地点からＡが歩き始め、その１８分後にＢがＰ地点からＡと同じ向きに歩き始め、さらにその１３分後にＣがＰ地点から２人と反対向きに歩き始めました。次のことが起こるのは、Ａが歩き始めてからそれぞれ何分後ですか。
① Ｂが初めてＡを追いこす
② ＡとＣが初めて出会う
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
Ａが２周するのにかかる時間とＢが３周するのにかかる時間が等しいので、その時間を２と３の最小公倍数である⑥とおき、ＡとＢがそれぞれ池を１周するのにかかる時間の割合を求めてみます。
Ａは池を２周するのに⑥の時間がかかるので、１周するのにかかる時間は⑥÷２＝③と表せます。
また、Ｂは池を３周するのに⑥の時間がかかるので、１周するのにかかる時間は⑥÷３＝②と表せます。
このとき、Ｃが池を２周するのにかかる時間は②＋２０分と表せるので、Ｃが１周するのにかかる時間は(②＋２０分)÷２＝①＋１０分となります。
つまり次の図のように、３人が池を１周するのにかかる時間の合計は、③＋②＋(①＋１０分)＝⑥＋１０分と表すことができます。
また、それが１時間３４分＝９４分にあたるので、⑥＋１０分＝９４分という式が作れます。
※ 画像はすべて、クリックすると拡大します。
このとき、９４－１０＝８４分が比の⑥にあたるので、比の①は８４÷⑥＝１４分です。
Ｃが池を１周するのにかかる時間は①＋１０分なので、答えは１４＋１０＝２４分になります。
(２)
まずはこの３人が同じ距離を進むのにかかる時間の比を求め、それを逆比にして速さの比を求めます。
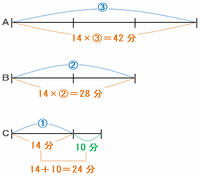
さっきの問題で比の①が１４分にあたることが分かったので、次の図のように、Ａが池を１周するのにかかる時間は１４×③＝４２分、Ｂが池を１周するのにかかる時間は１４×②＝２８分になります。
したがって、この３人が同じ距離を進むのにかかる時間の比は、Ａ：Ｂ：Ｃ＝４２：２８：２４＝２１：１４：１２となります。
時間の比を逆比にすると速さの比になるので、この３人の速さの比はＡ：Ｂ：Ｃ＝２１分の１：１４分の１：１２分の１と表せます。
その３つの数に２１と１４と１２の最小公倍数である８４をかけてそれぞれ整数に直すと、Ａ：Ｂ：Ｃ＝４：６：７になります。
(３)の①
３人の速さをＡ＝４、Ｂ＝６、Ｃ＝７と考え、旅人算の公式を使って答えを求めます。
次の図のように、Ａは１８分間で４×１８＝７２進みます。
Ｂが進み始めると、その差は１分間に６－４＝２ずつ縮まっていくので、ＢがＡに追いつくのはＢが出発してから７２÷２＝３６分後です。
ただし、この問題はＡがＰ地点を出発してからの時間を求める問題なので、答えは１８＋３６＝５４分後になります。
(３)の②
毎分４ずつ進むＡが４２分歩くと池を１周できるので、この池のまわりの長さは４×４２＝１６８と表せます。
また、ＣがＰ地点を出発するまでの１８＋１３＝３１分間に、Ａは４×３１＝１２４進むので、Ｃが出発するときの２人は次の図のように１６８－１２４＝４４離れています。
上の図の状態からＡとＣが出会うまでにかかる時間は、４４÷(４＋７)＝４分です。
ただし、Ｃが出発する前にＡは１８＋１３＝３１分進んでいるので、答えは３１＋４＝３５分後になります。
PR
