次の図のように、赤、青、緑、黄、白の玉が２個ずつ、合計１０個の玉が入った袋があります。この袋に次のような操作を行います。
【操作】
まず、袋から３個の玉を取り出す。取り出した３個の玉について、２個が同じ色のとき、同じ色の２個を袋に戻し、３個とも異なる色のときは何も戻さない。
※ 画像はクリックすると拡大します。
例えば、１回目の操作で、取り出した玉が赤・赤・青のとき、赤２個を戻し、袋の中の玉の数は９個になります。さらに、２回目の操作で、取り出した玉が赤・青・緑のとき、袋の中の玉の数は６個になります。なお、袋の中の玉の数が２個以下のときは、操作は行えません。この操作をくり返すとき、次の問いに答えなさい。
(１)
この操作を何回か行ったところ、袋の中の玉の数は１０個から４個になりました。操作を行った回数として考えられるものをすべて答えなさい。
(２)
この操作を何回か行ったところ、袋の中の玉の数は１０個から０個になりました。操作を行った回数として考えられるものをすべて答えなさい。
(３)
この操作を４回行ったところ、袋の中の玉は１０個から「黄１個、白１個」の合計２個になりました。このとき、袋の中の玉の個数は、１０→○→△→□→２のように変化します。途中の個数の変化として考えられるものを、「○→△→□」のようにしてすべて答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
もし取り出した３個の玉が「赤・青・緑」のように３つとも異なる色だった場合は、袋の中の玉の数が３個減ります。
また、もし取り出した３個の玉が「赤・赤・青」のように１つだけ異なる色だった場合は、同じ色の２個は袋に戻すので、袋の中の玉の数は１個減ります。
つまり、１回の作業で袋の中から減る玉の数は「３個」または「１個」のどちらかなので、袋の中の玉の数を１０－４＝６個減らすには「３個」と「１個」をどのように組み合わせればＯＫなのかを考えてみると、
・「３個」ずつ２回
・「３個」を１回と「１個」を３回
・「１個」ずつ６回
の３パターンあることが分かります。
したがって、考えられる操作回数は、２回、１＋３＝４回、６回のいずれかになります。
(２)
もし袋の中に「赤・赤・青」のような１つだけ色の異なるパターンで３つの玉が残ってしまうと、赤い２つの玉は袋に戻さなければいけないので、袋の中にある玉を０個にすることはできません。
※ 玉が２つ以下のときはもう操作ができないから。
したがって、袋の中にある１０個の玉をすべて取り出すには、残り３個になった段階で「赤・青・緑」のようにすべての色が異なる組み合わせにして、最後の操作でその３つをすべて取り出せばＯＫです。
例えば次の図のように「赤・青・緑」の組み合わせを２つ作り、
・黄色い２個の玉を１個ずつ「赤・赤・黄」の組み合わせで取り出す(赤２個は毎回戻す)
・白い２個の玉も１個ずつ「赤・赤・白」の組み合わせで取り出す(赤２個は毎回戻す)
・残った「赤・青・緑」の２組を最後の２回ですべて取り出す
という流れで、すべての玉を２×３＝６回の操作で袋から取り出すことができます。
※ 画像はすべて、クリックすると拡大します。
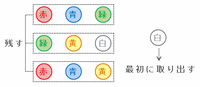
また、次の図のように１０個のうちの９個を「赤・青・緑」、「緑・黄・白」、「赤・青・黄」という色の異なる３つの組み合わせにして、
・まずは白い玉１個を「赤・赤・白」の組み合わせで取り出す(赤２個は戻す)
・「赤・青・緑」、「緑・黄・白」、「赤・青・黄」を１組ずつ取り出す
という流れで、すべての玉を１＋３＝４回の操作で袋から取り出すことができます。
以上から、答えは４回または６回のいずれかになります。
(３)
もし３回目の操作の後、袋の中に「赤・赤・黄」のような形で同じ色の玉が２個と異なる色の玉が１個入っていた場合、操作４の後は袋の中に同じ色の玉である「赤・赤」の２個が戻されたはずです。
しかしこの問題の場合、操作４の後に「黄・白」という異なる色の玉が１個ずつ袋の中に残ったので、４回目の操作では「赤・青・緑」のような異なる３つの色の玉が取り出されたことが分かります。
つまり、４回目の操作で袋から３個の玉を取り出したので、次の図の□には２＋３＝５個があてはまります。
また、操作１から３までの３回で、袋の中の玉は１０－５＝５個減ったことも分かります。
１回の操作で減る玉の数は「１個」または「３個」のどちらかしかないので、３回の操作にそのどちらかをあてはめて５個減る組み合わせを考えてみると、
・１個減る→１個減る→３個減る
・１個減る→３個減る→１個減る
・３個減る→１個減る→１個減る
の３通りが考えられます(次の図参照)。
上の図の３パターンは、どれも□には「５個」があてはまるので、それぞれの○と△にあてはまる数を調べてみると、
・「１個減る→１個減る→３個減る」のとき→○は１０－１＝９個、△は９－１＝８個
・「１個減る→３個減る→１個減る」のとき→○は１０－１＝９個、△は９－３＝６個
・「３個減る→１個減る→１個減る」のとき→○は１０－３＝７個、△は７－１＝６個
となることから、答えは「９→８→５」、「９→６→５」、「７→６→５」になります。
PR
