箱の中に６枚のカード「１」、「２」、「３」、「４」、「５」、「６」があります。箱の中からカードを１枚ずつ引いていき、取り出したカードを左から順に並べていく作業を行います。「５」が出るかまたは４枚のカードを並べたところでこの作業を終えるとき、次の問いに答えなさい。
(１)
このようなカードの並べ方は、全部で何通りありますか。
(２)
このようなカードの並べ方のうち、「１」を含む並べ方は全部で何通りありますか。
(３)
このようなカードの並べ方のうち、３枚目のカードを並べて終了した場合について考えます。並べたカードを左から順に、百の位、十の位、一の位として３けたの数として見たとき、考えられる数すべての和を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
大まかに言うと、「５」が１枚目に出た場合、２枚目に出た場合、３枚目に出た場合、４枚目に出た場合、そして４枚目にも出なかった場合の５つのパターンについて、それぞれ何通りあるのかを確認すればＯＫです。
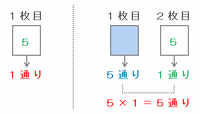
「５」が１枚目に出た場合はどう考えても１通りしかありませんが、「５」が２枚目に出た場合の組み合わせは、
・１枚目→「１」、「２」、「３」、「４」、「６」のどれか１枚を選ぶので５通り
・２枚目→「５」以外はダメなので１通り
となることから、５×１＝５通りになります(次の図参照)。
※ 画像はすべて、クリックすると拡大します。
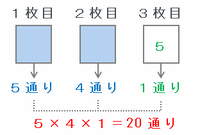
また、「５」が３枚目に出た場合の組み合わせは、
・１枚目→「１」、「２」、「３」、「４」、「６」のどれか１枚を選ぶので５通り
・２枚目→１枚目で選ばなかった４枚からどれか１枚を選ぶので４通り
・３枚目→「５」以外はダメなので１通り
となることから、５×４×１＝２０通りできます(次の図参照)。
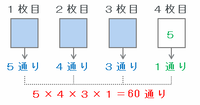
「５」が４枚目に出た場合の組み合わせは、
・１枚目→「１」、「２」、「３」、「４」、「６」のどれか１枚を選ぶので５通り
・２枚目→１枚目で選ばなかった４枚からどれか１枚を選ぶので４通り
・３枚目→１枚目と２枚目で選ばなかった３枚からどれか１枚を選ぶので３通り
・４枚目→「５」以外はダメなので１通り
となることから、５×４×３×１＝６０通りできます(次の図参照)。
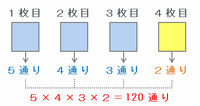
「５」が最後まで出なかった場合の組み合わせは、
・１枚目→「１」、「２」、「３」、「４」、「６」のどれか１枚を選ぶので５通り
・２枚目→１枚目で選ばなかった４枚からどれか１枚を選ぶので４通り
・３枚目→１枚目と２枚目で選ばなかった３枚からどれか１枚を選ぶので３通り
・４枚目→１～３枚目で選ばなかった２枚のどちらかなので２通り
となることから、５×４×３×２＝１２０通りできます(次の図参照)。
以上で５つのパターンがそれぞれ何通りできるのかが分かったので、答えは１＋５＋２０＋６０＋１２０＝２０６通りになります。
(２)
必ずどこかで「１」を使うのは、
・１枚目が「１」で２枚目が「５」の場合
・１枚目または２枚目が「１」で３枚目が「５」の場合
・１～３枚目のどれかが「１」で４枚目が「５」の場合
・１～４枚目のどこかで「１」を使い、残り３枚は「５」以外の場合
の４つのパターンが考えられますが、このうち、１枚目が「１」で２枚目が「５」となる場合は１通りしかありえません。
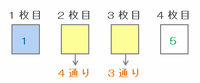
次の図のように、仮に１枚目を「１」、３枚目を「５」とすると、２枚目には「２」、「３」、「４」、「６」から１枚をあてはめるので４通りできます。
また、２枚目に「１」、３枚目を「５」を使った場合でも同じく４通りできるので、１枚目または２枚目が「１」で３枚目が「５」の場合は全部で４×２＝８通りあります。
次の図のように、仮に１枚目を「１」、４枚目を「５」とすると、
・２枚目→「２」、「３」、「４」、「６」から１枚をあてはめるので４通り
・３枚目→２枚目で使わなかった中から１枚をあてはめるので３通り
となるので４×３＝１２通りできます。
また、２枚目と３枚目にそれぞれ「１」を使った場合でも同じように１２通りずつできるので、１～３枚目のどれかが「１」で４枚目が「５」の場合は全部で１２×３＝３６通りできます。
次の図のように、仮に１枚目を「１」として、２枚目以降は「５」以外のカードをあてはめるとすると、
・２枚目→「２」、「３」、「４」、「６」から１枚をあてはめるので４通り
・３枚目→２枚目で使わなかった中から１枚をあてはめるので３通り
・４枚目→２枚目と３枚目で使わなかった２枚のどちらかなので２通り
となるので４×３×２＝２４通りできます。
また、２～４枚目にそれぞれ「１」を使った場合でも同じように２４通りずつできるので、１～４枚目のどこかで「１」を使い、残り３枚は「５」以外の場合は全部で２４×４＝９６通りできます。
以上で４つのパターンがそれぞれ何通りできるのかが分かったので、答えは１＋８＋３６＋９６＝１４１通りになります。
(３)
３枚目のカードを並べて終了するのは、３枚目に「５」が出て３けたの数「○△５」ができたときです。
また、(１)の問題で３枚目が「５」となるパターンは２０通りあることが分かったので、３けたの数「○△５」の一の位の合計だけを求めてみると、５×２０＝１００となります。
次の図のように、仮に百の位を「１」、一の位を「５」とすると、十の位には「２」、「３」、「４」、「６」のどれかがあてはまるので、３けたの数「１△５」は４通りできます。
また、百の位に「２」、「３」、「４」、「６」をあてはめた場合もそれぞれ４通りずつできるので、３けたの数「○△５」の百の位の合計だけを求めてみると、(１＋２＋３＋４＋６)×４×１００＝６４００になります。
次の図のように、仮に十の位を「１」、一の位を「５」とすると、百の位には「２」、「３」、「４」、「６」のどれかがあてはまるので、３けたの数「○１５」は４通りできます。
また、十の位に「２」、「３」、「４」、「６」をあてはめた場合もそれぞれ４通りずつできるので、３けたの数「○△５」の十の位の合計だけを求めてみると、(１＋２＋３＋４＋６)×４×１０＝６４０になります。
つまり、３けたの数「○△５」全部で２０個でき、百の位の合計は６４００、十の位の合計は６４０、そして一の位の合計は１００なので、２０個の数の合計は６４００＋６４０＋１００＝７１４０になります。
PR
