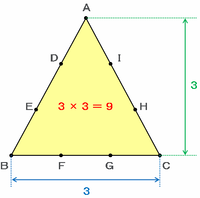
次の図のように、正三角形ＡＢＣのそれぞれの辺を３等分する点をＤ、Ｅ、Ｆ、Ｇ、Ｈ、Ｉとします。Ａ～Ｉのうち、３点を結んで三角形を作るとき、次の各問いに答えなさい。ただし、３点を結んで三角形ができないような結び方は考えないものとします。
※ 画像はクリックすると拡大します。
(１)
３点Ｅ、Ｆ、Ｉを結んでできる三角形の面積は正三角形ＡＢＣの何倍ですか。
(２)
３点を結んでできる三角形のうち、正三角形ＡＢＣの面積の３分の１となるものは何通りありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、三角形ＡＢＣの底辺の長さを３、高さを３とおくと、その面積は３×３＝９と表すことができます(÷２はすべての三角形で省略)。
※ 画像はすべて、クリックすると拡大します。
次の図を見れば分かるように、三角形ＥＦＩの面積は、三角形ＡＢＣの面積からＥＢＦ、ＩＦＣ、ＡＥＩの３つの三角形の面積を取り除けば求められます。
まずはその３つの三角形の面積をそれぞれ求めてみると・・・
・三角形ＥＢＦの面積→底辺と高さがそれぞれ１なので、１×１＝１
・三角形ＩＦＣの面積→底辺と高さがそれぞれ２なので、２×２＝４
・三角形ＡＥＩの面積→底辺が２、高さが１なので、２×１＝２
となるので、この３つの三角形の面積の合計は１＋４＋２＝７になります。
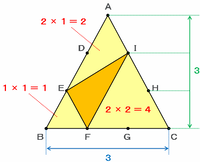
三角形ＡＢＣの面積は９、三角形ＥＦＩ以外の３つの三角形の面積は合わせて７なので、三角形ＥＦＩの面積は９－７＝２と表せます。
以上から、三角形ＥＦＩの面積は三角形ＡＢＣの２÷９＝９分の２倍になります。
(２)
三角形ＡＢＣの面積は９なので、面積が９÷３＝３になる三角形を探せばＯＫなのですが、それにあてはまる三角形は大きく２つのタイプに分けられます。
【その１ 真上からスパッと３等分してみる】
次の図のように、頂点ＡからナイフでＦとＧに向けてスパッと切りこみを入れることによって、面積３の三角形が３個できます。
※ 下の図の三角形ＡＢＦ、ＡＦＧ、ＡＧＣの３つ。
上の図のような分け方は、左側の辺ＡＢや右側の辺ＡＣが底辺となるようにクルッと向きを変えたときにも同じようにできるので、このタイプの三角形は全部で３×３＝９個できます。
【その２ 辺の途中にある点を結んでみる】
次の図の三角形ＤＢＦ、ＨＦＣ、ＡＤＨは、底辺と高さの組み合わせがどれも１と２なので、面積はすべて１×２＝２と表せます。
したがって三角形ＤＦＨの面積は９－２×３＝３になるので、問題文の条件にあてはまります。
また、これと同じ三角形は３点Ｅ、Ｆ、Ｉを結んでもできるので、このタイプの三角形は全部で２個できます。
以上から、面積が三角形ＡＢＣの３分の１になる三角形は全部で９＋２＝１１個になります。
PR
