正六角形の各頂点を反時計回りに順にＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆとし、３本の対角線ＡＤ、ＢＥ、ＣＦが交わる点をＧとします。これら計７つの点から３つの点を選び、それらを結んでできる三角形について、次の問いに答えなさい。ただし、三角形ＡＢＤのようにその辺上に４点目のＧがあっても構わないものとします。
(１)
何種類の三角形ができますか。ただし、合同な物は１種類として数えます。
(２)
全部で何個の三角形ができますか。ただし、(１)で数えた各種類ごとに分類して数え、その途中経過を簡潔に書きなさい。その場合、例えば三角形ＡＢＣと三角形ＢＣＤは２個として数えることとします。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは正六角形の中心にある点Ｇを使わない場合から考えてみます。
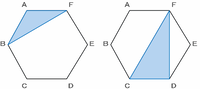
正六角形の２辺を使う場合、次の図のＡＢＦのような二等辺三角形ができます。また、正六角形の１辺を使う場合はＣＤＦのような直角三角形になります。
※ 画像はすべて、クリックすると拡大します。
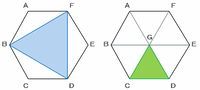
正六角形の外側の辺を使わない場合、次の図のＢＤＦのような大きい正三角形ができます。また、正六角形の中心である点Ｇを使う場合、下の図のＧＣＤのような小さい正三角形ができます。
以上から、３つの点を結んでできる三角形は全部で４種類になります。
(２)
問題文の指示の通り、さっき確認した４種類の三角形がそれぞれ何個あるのかを確認していきます。
【その１ 二等辺三角形の数を調べる】
次の図の青い二等辺三角形は、赤い頂点がＡからＦへ移動するごとに１個ずつできるので、全部で６個あります。
また、緑色の三角形は赤い頂点ＢとＦが「ＡとＣ」→「ＢとＤ」→「ＣとＥ」→「ＤとＦ」→「ＥとＡ」と動くごとに１個ずつできるので、こちらも全部で６個あります。
【その２ 直角三角形の数を調べる】
たとえば次の図のように赤い辺ＣＤを底辺とすると、オレンジ色と青色の直角三角形ができます。
つまり、正六角形の６つの辺を底辺とするごとに直角三角形が２個ずつできるので、直角三角形は全部で６×２＝１２個になります。
【その３ 大きい正三角形の数を調べる】
正六角形の頂点を１個飛ばしに３個選んで結ぶと、次の図のような大きい正三角形ＢＤＦとＡＣＥができます。
【その４ 小さい正三角形の数を調べる】
正六角形の中心Ｇを必ず使って三角形を作るとき、次の図のように小さい正三角形が全部で６個できます。
これまでの流れを振り返ってみると、
・二等辺三角形→６×２＝１２個できる
・直角三角形→６×２＝１２個できる
・大きい正三角形→２個できる
・小さい正三角形→６個できる
となることが分かったので、三角形は全部で１２＋１２＋２＋６＝３２個できます。
PR
