各面に１から６までの整数が１ずつ書かれたサイコロが１個あります。このサイコロをふったときに、出た目の数を次のように書きかえます。
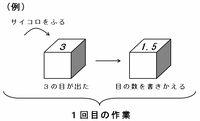
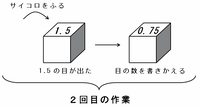
※ 画像はすべて、クリックすると拡大します。
たとえば下の(例)のように、サイコロをふって３の目が出たら１.５に書きかえます。さらに、このサイコロをふって１.５の目が出たら０.７５に書きかえます。
サイコロをふってから目の数を書きかえるまでの作業を１回と数えるとき、次の問いに答えなさい。
(１)
６回の作業を行ったのち、サイコロの面に書かれている数を合計します。合計した数のうち、最も小さい値を求めなさい。
(２)
何回かの作業を行ったのち、６つの面は次のようになりました。
このとき、何回の作業を行いましたか。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
サイコロの目の合計をなるべく小さくするために、まずは「６」「５」「４」などの大きい数を半分の数に書きかえると、それぞれ「３」「２.５」「２」となります。
この時点で、サイコロの６つの目は次のようになっています。
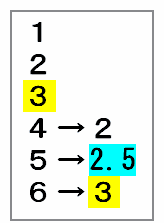
※ 画像はすべて、クリックすると拡大します。
上の図にある２つの「３」が最も大きい数なので、どちらも半分の数である「１.５」に書きかえます。
すると今度は「２.５」が最大になるので、半分の数である「１.２５」に書きかえます。
以上で６回目の作業が終わり、サイコロの目は次の図のようになりました。
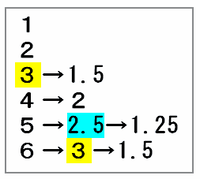
したがって、サイコロの目の最小値は１＋２＋１.５＋２＋１.２５＋１.５＝９.２５になります。
(２)
６つの面の結果についてまとめると、次のようになります。
① １.２５の目が１面→「５→２.５→１.２５」なので、作業２回。
② ３の目が２面→もともとの「３」と「６→３」なので、作業１回。
③ １の目が２面→もともとの「１」と、「２→１」または「４→２→１」のどちらか。
④ ２の目が１面→もともとの「２」または「４→２」のどちらか。
ここで③と④の関係について考えてみると、
・もし③が「２→１」なら、④は「４→２」になるので、作業は合わせて２回。
・もし③が「４→２→１」なら、④はもともとの「２」になるので、作業は合わせて２回。
となり、どちらにしても③と④で合わせて２回の作業が行われたことに変わりはありません。
以上から、作業の合計は２＋１＋２＝５回になります。
PR
