大きさの異なる正方形のカードを、図のようにある規則にしたがってならべる。それぞれのカードには、１㎝四方のます目が書いてあり、左上のます目から１、２、３、・・・と順番に数が書かれている。次の( )にあてはまる数を答えなさい。
なお、「左上のます目の数」とは、１番目のカードでは１、２番目のカードでは７、３番目のカードでは２１のことである。
※ 画像はクリックすると拡大します。
(１)
１辺が２１㎝のカードの「左下のます目の数」は( )である。
(２)
「左下のます目の数」が１０５７であるカードは、( )番目のカードである。
(３)
「左下のます目の数」の１の位が３であるカードは、１番目から１００番目までの１００枚のカードの中に( )枚ある。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは次の図を使って、１辺の長さやます目の数などの規則性を確認しておくと、
・□番目の１辺の長さ→１番目は１㎝、２番目は３㎝、３番目は５㎝のように、□番目の１辺の長さは(□番目の奇数)㎝になる。
・□番目のます目の数→１番目は１×１＝１個、２番目は２×２＝４個、３番目は３×３＝９個のように、□番目のます目の数は(□番目の奇数)×(□番目の奇数)を計算すれば求められる。
となっています。
※ 画像はすべて、クリックすると拡大します。
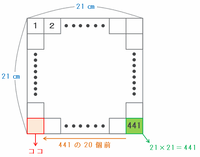
１辺の長さが２１㎝のときは、次の図のようにカードの右下に２１×２１＝４４１があり、左下のます目にはそこから２０個前の数があてはまります。
したがって、１辺２１㎝のカードの左下には４４１－２０＝４２１があてはまります。
(２)
まずは(同じ数)×(同じ数)の答えが１０５７にいちばん近くなる場合を考えてみると、
・３０×３０＝９００→手前過ぎ
・４０×４０＝１６００→行き過ぎ
・３５×３５＝１２２５→もうちょい手前
・３３×３３＝１０８９→かなり近い
という感じなので、次のような１辺３３㎝のカードの図を使って確かめてみます。
上の図の左下のます目には、１０８９の３２個手前にある数があてはまります。
１０８９－３２＝１０５７でピッタリなので、左下のます目が１０５７となるカードは１辺の長さが３３㎝であることが分かります。
このとき、３３は(３３＋１)÷２＝１７番目の奇数なので、１辺の長さが３３㎝となるのは１７番目のカードのときです。
(３)
１番目から３番目までのカードは条件にあてはまらないのですが、４番目と５番目のカードは、次の図のように左下のます目に１の位が「３」となる数字が来ています。
つまり、１番目から５番目のカードの中で条件にあてはまるものは２つあるのですが、次の図のように６番目から１０番目のカードを調べてみると、条件にあてはまるものがやはり２つあることが分かります。
ここまでの流れを振り返ってみると、「１番目から５番目まで」と「６番目から１０番目まで」はどちらも「×・×・×・○・○」となっていることから、条件にあてはまるのは５個の中に２つずつあることが分かります。
１００÷５＝２０組なので、１番目から１００番目までの中で、左下のます目の１の位に「３」が出てくるカードは、全部で２×２０＝４０枚あります。
PR
