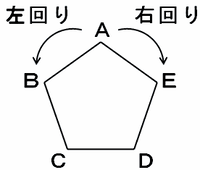
正五角形ＡＢＣＤＥと白玉、黒玉が１個ずつあります。白玉は右回りに、黒玉は左回りに、頂点から頂点へ同じ速さで移動します。１回の移動で３つ先の頂点まで進み、止まります。次の移動からは、直前の移動で止まった場所から進みます。
白玉も黒玉もそれぞれ出発した頂点に止まったら、それ以上移動することはできません。このとき、次の各問いに答えなさい。
(１)
白玉が頂点Ａから移動を始めた場合、何回まで移動することができますか。
(２)
黒玉が頂点Ｅから移動を始めた場合、何回まで角を曲がることができますか。
(３)
白玉と黒玉が同時に出発し、白玉、黒玉が最後にすれ違った場所が頂点Ｃと頂点Ｄのちょうど真ん中でした。白玉と黒玉は、それぞれどの頂点から出発しましたか。考えられるだけすべてあげなさい。例えば、白玉が頂点Ｂで、黒玉が頂点Ｃの場合、(白、黒)＝(Ｂ、Ｃ)と表しなさい。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
正五角形には頂点が全部で５個あるので、白玉は正五角形のまわりを１周するたびに頂点を５個ずつ進みます。
また、白玉は１回で頂点を３個進むので、５と３の最小公倍数である１５個目の頂点まで進んだとき、ちょうど出発点で止まることになります。
したがって、白玉は１５÷３＝５回まで移動することができます(次の図)。
※ 画像はすべて、クリックすると拡大します。
(２)
次の図を見れば分かるように、角を曲がる回数は進んだ頂点の数よりも１少なくなります。
黒玉もさっきの白玉と同じように、スタート地点で止まるまでに頂点を１５個進むので、角を曲がった回数は全部で１５－１＝１４回になります。
(３)
白玉も黒玉もそれぞれ「ワン！ツー！スリー！」という感じで頂点を３個ずつ進んでいくのですが、最後にＣとＤの真ん中ですれ違ったときが「ワン！」「ツー！」「スリー！」のどれだったのかによって、次の①～③の３つの図に分かれます。
① おたがいの「ワン！」のときにすれ違う場合
おたがいの「ワン！」のときにＣＤの真ん中ですれ違う場合、上の①の図のように白玉はＤからＣ→Ｂ→Ａ、黒玉はＣからＤ→Ｅ→Ａの順に進みます。
このとき、どちらの玉もＡで終わっているのですが、終着点は出発点でもあるので、出発した頂点は(白、黒)＝(Ａ、Ａ)と表せます。
② おたがいの「ツー！」のときにすれ違う場合
おたがいの「ツー！」のときにＣＤの真ん中ですれ違う場合、上の②の図のように白玉はＥからＤ→Ｃ→Ｂ、黒玉はＢからＣ→Ｄ→Ｅの順に進みます。
このとき、２つの玉が出発した頂点は(白、黒)＝(Ｂ、Ｅ)と表せます。
③ おたがいの「スリー！」のときにすれ違う場合
おたがいの「スリー！」のときにＣＤの真ん中ですれ違う場合、上の③の図のように白玉はＡからＥ→Ｄ→Ｃ、黒玉はＡからＢ→Ｃ→Ｄの順に進みます。
このとき、２つの玉が出発した頂点は(白、黒)＝(Ｃ、Ｄ)となります。
PR
