偶数２、４、６、８、１０、・・・・・を次のルールにしたがって、下の表にならべます。
※ 画像はすべて、クリックすると拡大します。
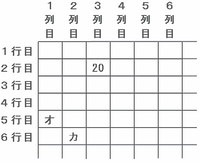
【ルール】
① 偶数を商が奇数になるまで２で何回も割ります。
② ２で割ることができた回数をＸ、奇数の商に１を加えて再び２で割った商をＹとします。
③ その偶数をＸ行目のＹ列目にならべます。
たとえば、２０は
２０÷２＝１０、１０÷２＝５、(５＋１)÷２＝３なので、Ｘ＝２、Ｙ＝３ですから、２行目の３列目にならべます。
次のア～シにあてはまる数を求めなさい。
(１) ２４はア行目のイ列目にくる数です。
(２) ５０はウ行目のエ列目にくる数です。
(３) ５行目の１列目にくる数はオです。
(４) ６行目の２列目にくる数はカです。
(５) キ、ク、ケが次の図のようにならんでいます。クはキよりも１６だけ大きくケよりも５６だけ小さいです。
(６) コ、サ、シが次の図のようにならんでいます。コ＋サ＋シ＝４０３２です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
問題文で説明されたルールが理解できているかどうかを確認するための問題です。
２４をひたすら２で割っていくと、２４÷２＝１２、１２÷２＝６、６÷２＝３となります。
つまり２４は２で３回割れるので、Ｘには３があてはまります。
そして、最後に２で割ったときの商である「３」に１を加えて２で割ると、(３＋１)÷２＝２になるので、Ｙには２があてはまります。
以上から、２４は３行目の２列目にあてはまる数であることが分かったので、ア＝３、イ＝２になります。
(２)
まずはさっきの問題と同じように５０を２で割ってみると、５０÷２＝２５となるので、５０は２で１回しか割れません。
また、そのときの商である「２５」に１を加えて２で割ると、(２５＋１)÷２＝１３になります。
つまり、５０は１行目の１３列目にあてはまる数なので、ウ＝１、エ＝１３になります。
(３)
５行目の１列目にくる数には、
・２で５回まで割れる
・２で５回目に割ったときの商を□とすると、(□＋１)÷２＝１となる
という２つの特徴があります。
まずは(□＋１)÷２＝１の□にあてはまる数を求めると、１×２－１＝１となります。
５行目の１列目にくる数を△とおくと、それを２で５回割ると商が１になることから、△÷２÷２÷２÷２÷２＝１という式に表すことができます。
つまり、△には１×２×２×２×２×２＝３２があてはまるので、オ＝３２となります。
(４)
さっきの問題と同じように６行目の２列目にくる数の特徴を確認してみると、次のようになります。
・２で６回まで割れる
・２で６回目に割ったときの商を□とすると、(□＋１)÷２＝２となる
まずは(□＋１)÷２＝２の□にあてはまる数を求めると、２×２－１＝３となります。
６行目の２列目にくる数を△とおくと、それを２で６回割ると商が３になることから、△÷２÷２÷２÷２÷２÷２＝３という式に表すことができます。
その式を逆算すると３×２×２×２×２×２×２＝１９２になるので、カ＝１９２となります。
(５)
まずは規則性を見つけるため、次の図のようにある程度までこの表に数をうめてみます。
※ 画像はすべて、クリックすると拡大します。
特にそれぞれの列を縦に見てみると、下のマス目の数は上のマス目の数の２倍になっていることが分かります。
※ 例えば６は２×３、その下にある１２は２×２×３、さらにその下の２４は２×２×２×３、・・・のように、下に進むにしたがって「×２」が１個ずつ増えていきます。
つまり、次の図のケはクの２倍の数なので、クにあてはまる数の大きさを①とおくと、ケの大きさは②と表せます。
また、ケはクよりも５６大きいので、次の線分図の②－①＝①めもりが２つの数の差である５６にあたります。
以上から、クは①めもりなので５６、ケはその２倍である１１２、そしてキはクよりも１６小さいので４０になります。
(６)
次の図のように、サはコの２倍、そしてシはサの２倍の数なので、コにあてはまる数の大きさを①とおくと、サは①×２＝②、シは②×２＝④と表すことができます。
したがって、コを①めもりとおいて３つの数の大きさを線分図に表すと下のようになります。
また、コ＋サ＋シ＝４０３２になることも分かっているので、それも線分図の右側に書き込んでおきます。
上の図の①＋②＋③＝⑦が３つの数の合計である４０３２にあたるので、コは４０３２÷⑦＝５７６になります。
また、サはその２倍なので５７６×２＝１１５２、シはさらにその２倍なので１１５２×２＝２３０４になります。
PR
