次の図のＡＤの長さは何㎝ですか。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
カッコよく補助線を引くとサクサク解けて気持ちのいい問題です。
「６０度といえば正三角形のひとつの内角だよなー」と気がつけば、どんな補助線を引くのか見当がつけやすいと思います。
まずは次の図のように赤い直線ＢＥを引きます。辺ＢＥは辺ＡＢ同じく長さが２㎝で、しかも辺ＡＣと平行になるようにします。
ついでに点Ｄと点Ｅも赤い直線で結ぶと、角ＣＡＤと角ＢＥＤは錯角の関係なのでどちらも６０度です。
また、角ＡＤＣと角ＢＤＥも対頂角の関係なので大きさが等しくなっています。
つまり、三角形ＡＤＣと三角形ＥＤＢは２つの内角の大きさが等しい(つまり残り１つの内角の大きさも同じになる)ので、この２つの三角形は８の字相似になります。
※ 画像はすべて、クリックすると拡大します。
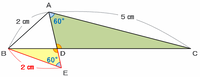
次は下の図の三角形ＡＢＥに注目してみると、この三角形は辺ＡＢと辺ＢＥの長さが等しいだけでなく、２つの内角が６０度(つまり残り１つの内角も６０度)なので、二等辺ではなく正三角形であることが分かります。
したがって、下の図の辺ＡＥの長さは２㎝になります。
三角形ＡＤＣと三角形ＥＤＢは、次の図のように辺ＡＣと辺ＢＥの長さの比が５：２なので、下の図の辺ＡＤと辺ＤＥの長さの比もそれと同じく５：２になっているはずです。
したがって、辺ＡＤの長さを求めるためには、辺ＡＥの長さである２㎝を５：２に比例配分してやればＯＫです。
※ ここからは計算に分数が出てくるので、求め方を画像に変換します。
PR
