連続した２５個の整数があり、そのうち偶数だけの和から奇数だけの和を引くと４４になりました。この２５個の整数の和は( )です。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
この２５個の整数が奇数と偶数のどちらから始まっているのかを読み取るため、まずは次の２つのケースで規則性を確認してみます。
※ 画像はすべて、クリックすると拡大します。
【奇数から始まる数列の場合】
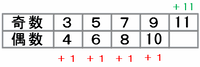
たとえば３から１１までの９個の整数で奇数と偶数の合計を比べてみると、上の表のように最初から４組目までは偶数が１ずつリードを積み上げるのですが、最後に奇数の１１があるので、結局は奇数の合計が偶数よりも１１－１×４＝７大きくなります。
※ このとき、奇数の最後の数は７＋４＝１１という計算で求められます。
【偶数から始まる数列の場合】
今度は１から１０までの１０個の整数で偶数と奇数の合計を比べてみると、上の表のように最初から４組目までは奇数が１ずつリードを積み上げるのですが、最後に偶数の１０があるので、結局は偶数の合計が奇数よりも１０－１×４＝６大きくなります。
※ このとき、偶数の最後の数は６＋４＝１０という計算で求められます。
以上から、この数列は奇数の和の方が大きければ奇数から、偶数の和の方が大きければ偶数からスタートしていることが分かります。
この問題の場合、偶数の和の方が奇数の和よりも大きいので、次の表のように偶数からスタートしています。
また、整数は全部で２５個なので、最後の偶数を除けば偶数と奇数の組み合わせが(２５－１)÷２＝１２組あることも分かります。
最初の１２組で奇数は１ずつリードし、偶数よりも合計が１２大きくなっています。しかし最後に偶数の□があるので、合計は偶数が奇数よりも□－１２＝４４大きくなりました。
このとき、最後の偶数である□は４４＋１２＝５６なので、最初の偶数は５６－２４＝３２になります。
つまりこの数列は３２から５６までの２５個の整数なので、その和は(３２＋５６)×２５÷２＝１１００になります。
PR
