スタート地点からゴール地点までの途中２か所に、休息所Ｐ地、Ｑ地があります。Ａ君、Ｂ君、Ｃ君は正午に出発し、それぞれＰ地までは一定の速さで歩くものとします。Ｃ君がＰ地へ一番早く、午後２時４８分に着き、Ｃ君の到着より２１分遅れてＢ君が着き、Ｂ君の到着よりさらに２７分遅れてＡ君が着きました。
Ａ君は休まずＢ君と一緒にＰ地を出て、最初のＢ君の速さで歩いたので、午後５時４２分にＱ地に着きました。Ａ、Ｂ両君はそこで２０分休息し、今度は最初のＡ君の速さでゴールまで歩いたので、午後７時１４分にゴールしました。このとき、次の問いに答えなさい。
(１)
Ａ君、Ｂ君、Ｃ君３人の最初の速さの比を最も簡単な整数の比で表しなさい。
(２)
スタート地点からＰ地、Ｐ地からＱ地、Ｑ地からゴール地点までの距離の比を最も簡単な整数の比で表しなさい。
(３)
Ａ君の最初の速さが毎時４.９㎞とすれば、スタート地点からゴール地点までは何㎞ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように３人はそろって正午にスタート地点から出発し、Ｃ君は午後２時４８分、Ｂ君はそれよりも２１分遅い午後３時９分、Ａ君はさらに２７分遅い午後３時３６分にＰ地点へ到着しました。
※ 画像はすべて、クリックすると拡大します。
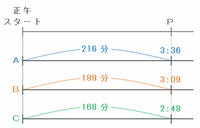
上の図で３人がスタート地点からＰ地点まで進むのにかかった時間をそれぞれ求めてみると、Ａ君は３時間３６分＝２１６分、Ｂ君は３時間９分＝１８９分、Ｃ君は２時間４８分＝１６８分です。
つまり、この３人が同じ距離を進むのにかかる時間の比はＡ：Ｂ：Ｃ＝２１６分：１８９分：１６８分＝７２：６３：５６となるので、その逆比を求めれば３人の最初の速さの比が分かります。
７２：６３：５６の逆比は７２分の１：６３分の１：５６分の１となるのですが、７２は８×９、６３は７×９、５６は７×８と表せるので、３つの分数の分母の最小公倍数は「７×８×９」であることが分かります。
したがって、次の図のように３つの分数へそれぞれ「７×８×９」をかけ合わせてみると、
・７２分の１→分母は「８×９」、分子は「７×８×９」なので、分子に７だけが残る。
・６３分の１→分母は「７×９」、分子は「７×８×９」なので、分子に８だけが残る。
・５６分の１→分母は「７×８」、分子は「７×８×９」なので、分子に９だけが残る。
となることから、３人の最初の速さの比はＡ：Ｂ：Ｃ＝７：８：９となります。
(２)
次の図のように、ＡとＢの２人はＰＱ間をＢの速さである８で、そしてＱ地点からゴールまではＡの速さである７で一緒に進みました。
また、２人がＰＱ間を進むのにかかった時間は５時４２分－３時３６分＝２時間６分＝１２６分、そしてＱ地点からゴールまで進むのにかかった時間は７時１４分－６時２分＝１時間１２分＝７２分です。
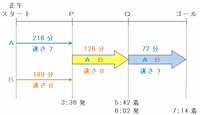
上の図を利用して３つの区間の距離をそれぞれ式で表してみると次のようになります。
・スタートからＰ地点→Ｂが８の速さで１８９分かかったので、８×１８９
・Ｐ地点からＱ地点→２人が８の速さで１２６分かかったので、８×１２６
・Ｑ地点からゴール→２人が７の速さで７２分かかったので、７×７２
つまり、「８×１８９」と「８×１２６」と「７×７２」の比を求めれば３つの区間の距離の比が分かるので、次の図のように約分っぽい作業をしてカンタンな比に直してみると、
・８×１８９→８で割ると１８９→９で割ると２１→７で割ると３
・８×１２６→８で割ると１２６→９で割ると１４→７で割ると２
・７×７２→８で割ると７×９→９で割ると７→７で割ると１
となることから、「スタートからＰ地点」と「Ｐ地点からＱ地点」と「Ｑ地点からゴール」までの距離の比は３：２：１です。
(３)
３つの区間の距離の比は３：２：１なので、スタート地点からゴールまでの距離は、次の図のように３＋２＋１＝６と表せます。
また、Ａ君はＱ地点からゴールまでの区間を時速４.９㎞で７２分＝１.２時間かけて進んだので、Ｑ地点からゴールまでの距離は４.９×１.２＝５.８８㎞です。
つまり、上の図の比の１が５.８８㎞にあたるので、スタート地点からゴールまでの距離(比の６)は５.８８×６＝３５.２８㎞になります。
PR
