次の図のような、たてと横の長さの比が３：５の長方形の形をしたランニングコースを、ＪさんはＡ地点から反時計回りに、ＧさんはＤ地点から時計回りに同時に出発し、２周しました。
※ 画像はクリックすると拡大します。
Ｊさんは１周１６分の速さで走り、途中Ａ地点で２分休み、Ｇさんは１周２０分の速さで走り、途中Ｄ地点で１分休みました。２人が１回目に出会ったのはＥ地点でした。ランニングコースの１周は( )ｍ、２人が２回目に出会った地点はＥ地点から( )ｍ離れています。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
【周りの長さの求め方】
ＪさんとＧさんが同じ距離を進むのにかかる時間の比は、Ｊ：Ｇ＝１６分：２０分＝４：５なので、２人の速さの比はＪ：Ｇ＝５：４になります。
※ 時間の逆比は速さの比。
つまり次の図のように、２人が同時に出発してから出会うまでに進んだ距離である「ＡＢ＋ＢＥ」と「ＤＣ＋ＣＥ」の長さの比も５：４なので、図の「ＡＢ＋ＢＣ＋ＣＤ」の長さは比の５＋４＝９となります。
※ 画像はすべて、クリックすると拡大します。
また、このコースのたてと横の長さの比は３：５なので、次の図のように辺ＡＢとＣＤの長さは比の３、そしてＢＣの長さは比の５と表せます。
したがって、図の「ＡＢ＋ＢＣ＋ＣＤ」の長さを比で表すと３＋５＋３＝１１となります。
同じコースの距離を表しているはずなのに、「ＡＢ＋ＢＣ＋ＣＤ」の長さの比が一方では９、もう一方では１１となってしまったので、その２種類の比を次の図のように９と１１の最小公倍数である９９にそろえてみると、
・「ＡＢ＋ＢＥ：ＤＣ＋ＣＥ＝５：４」を１１倍→ＡＢ＋ＢＥ：ＤＣ＋ＣＥ＝５５：４４
・「ＡＢ：ＢＣ：ＣＤ＝３：５：３」を９倍→ＡＢ：ＢＣ：ＣＤ＝２７：４５：２７
となります。
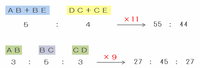
上の図から、ＡＢの長さは比の２７、ＡＢ＋ＢＥの長さは比の５５と表せることが分かったので、ＢＥの長さは比の５５－２７＝２８になります。
つまり次の図のように、ＢＥの長さである７００ｍが比の２８にあたるので、比の１は７００÷２８＝２５ｍです。
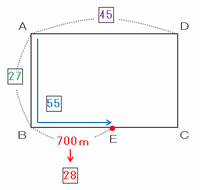
また、長方形のたての長さ(ＡＢやＤＣ)は比の２７、横の長さ(ＢＣ)は比の４５なので、長方形の周りの長さは比の(２７＋４５)×２＝１４４と表せます。
比の１は２５ｍなので、周りの長さは２５×１４４＝３６００ｍになります。
※ 次の問題に備えて、長方形のたてと横の長さをそれぞれ求めておくと、たては２５×２７＝６７５ｍ、横は２５×４５＝１１２５ｍになります。
【Ｅ地点からの距離の求め方】
２人ともコースを１周するのにかかる時間が分かっているので、とりあえず２人の速さをそれぞれ求めておくと、
・Ｊさん→３６００ｍを１６分で進むので、３６００÷１６＝分速２２５ｍ
・Ｇさん→３６００ｍを２０分で進むので、３６００÷２０＝分速１８０ｍ
となります。
また、１回目の出会いはＥ地点なので、２回目がどこだったのかを見つけるために、とりあえず２人がスタートしてから１６分後の位置関係を確かめてみると、
・Ｊさん→コースをちょうど１周して、Ａ地点に到着したところ
・Ｇさん→１８０×１６＝２８８０ｍ、２８８０－(６７５＋１１２５＋６７５)＝４０５ｍなので、Ａ地点から右へ４０５ｍ進んだところ
となります。
つまり次の図のように、２人が出発してから１６分後だと、すでに辺ＡＤ上で２回目の出会いを終えた後なので、時間を巻き戻して出会った地点を調べてみます。
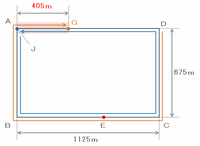
１６分後の状態から時間を巻き戻すと、次の図のようにＪさんは右へ分速２２５ｍで、Ｇさんは左へ１８０ｍでそれぞれ戻ります。
下の図から時間を４０５÷(２２５＋１８０)＝１分巻き戻すと２人は出会うので、２回目に出会ったのは２人が出発してから１６－１＝１５分後であり、その地点はＡから右へ２２５×１＝２２５ｍの地点であることも分かります。
１回目に出会った地点はＥなので、２回目に出会った地点は次の図のようにＦとすると、ＢＥは７００ｍ、ＡＢは６７５ｍ、そしてＡＦは２２５ｍなので、ＥとＦの間は７００＋６７５＋２２５＝１６００ｍ離れています。
また、このコースは１周３６００ｍなので、ＥからＦへ反時計回りで進むと３６００－１６００＝２０００ｍ離れています(どちらを答えてもＯＫ)。
【補足】
問題文にある「ＪさんはＡ地点で１分休んだ」とか「ＧさんはＤ地点で２分休んだ」という条件をまったく使わずに解けてしまったのでなんだか拍子抜けです(笑)
この問題を作った人は、たぶん３回目に出会ったときのことを出題したかったんじゃないかなー、と思う今日この頃です。
PR
