西から東へ向かう２車線の高速道路があります。ここを走る車は、Ａ、Ｐ、Ｑ、Ｂの４地点をこの順に通過しますが、Ｐ地点とＱ地点の間は工事をしているため、１車線は車が通れません。この日、たろうさん、ゆきおさん、しげるさんの３人がこの順にＡ地点とＢ地点の間を走りました。太郎さんは朝早かったため、渋滞には出くわさず、Ａ地点とＢ地点の間を１３分で走りました。ゆきおさんはＰ地点で渋滞に出くわし、Ａ地点とＢ地点の間を２２分で走りました。しげるさんが走ったときには、渋滞の長さがゆきおさんのときのちょうど２倍になっていました。走る車の速度は、２車線とも走ることができる場合は分速１２００ｍ、１車線しか走ることができない場合は分速８００ｍ、渋滞している場合は車線の数に関係なく分速２００ｍとします。また、渋滞の先頭はいつでもＱ地点で、ここを過ぎると渋滞は解消されるものとします。このとき、次の各問いに答えなさい。
※ 画像はクリックすると拡大します。
(１) Ａ地点とＢ地点の間の距離は何㎞ですか。
(２) しげるさんはＡ地点とＢ地点の間を走るのに何分かかりましたか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずはたろうさんとゆきおさんがＡＢ間を進むのにかかった時間差を利用して、ＰＱ間の距離を求めてみます。
次の図１のように、たろうさんはアとウの区間を分速１２００ｍで、そしてイの区間を分速８００ｍで進んだ結果、ＡＢ間を１３分で通過しました。
※ 画像はすべて、クリックすると拡大します。
次の図２のように、ゆきおさんはアとウの区間を分速１２００ｍで、そしてイの区間を分速２００ｍで進んだ結果、ＡＢ間を２２分で通過しました。
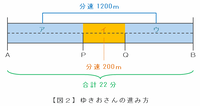
この２つの図はアとウにかかった時間は変わらない(速さも距離も同じ)ので、２人がＡＢ間を進むのにかかった時間の差である２２－１３＝９分は、イの区間の進み方によって生じたものであることが分かります。
２人がイの区間を進む速さの比は、たろう：ゆきお＝分速８００ｍ：分速２００ｍ＝４：１なので、２人がイの区間を進むのにかかる時間の比は、たろう：ゆきお＝１：４になります。
※ 速さの逆比は時間の比。
つまり、その時間の比の差である４－１＝３が、２人がイの区間を進むのにかかった時間の差である９分にあたるので、比の１は９÷３＝３分になります。
つまり、たろうさんはイの区間を分速８００ｍで３分かけて進んだので、その距離は８００×３＝２４００ｍになります。
また、たろうさんは次の図のようにアとウの区間を合わせて１３－３＝１０分かけて進んだことも分かるので、その２区間の距離の合計は１２００×１０＝１２０００ｍになります。
つまり、上の図のアとウは合わせて１２０００ｍ＝１２㎞、イは２４００ｍ＝２.４㎞なので、ＡＢ間の距離は１２＋２.４＝１４.４㎞になります。
(２)
しげるさんがＡＢ間を走ったときは、渋滞の区間が２４００×２＝４８００ｍになっていたので、次の図のアとウ(分速１２００ｍで走行した区間)は合わせて１４４００－４８００＝９６００ｍであることが分かります。
渋滞区間を通過するのにかかる時間は４８００÷２００＝２４分、そして残りの区間を通過するのにかかる時間は９６００÷１２００＝８分なので、しげるさんはＡＢ間を２４＋８＝３２分で通過しました。
PR
