気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
04/09
Fri
2010
桜蔭2010【3】 ☆速さ☆
最初が平らな道、中間が山道、最後が平らな道である全長10kmの徒歩コースがあります。このとき次の問いに答えなさい。
(1)
このコースを、平らな道は毎時6km、山道は毎時4kmで進むとあわせて1時間52分かかります。コース中間の山道は何kmですか。
(2) 最初(1)の速さで進み、ある地点からその後ずっと速さを(1)の半分にして進むと、2時間10分かかります。ただし、速さを変える地点は平らな道の上とします。速さを変える地点は、コースの出発地点から何kmのところですか。
※ 解説を見たい場合は、下の「解説はこちらから」をクリック!
(1)
この徒歩コースの全体は、だいたい次の図のようになっています。
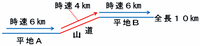
(画像はすべて、クリックすると拡大します)

つまり、山道を進むのに時速4kmで0.6時間かかるので、4×0.6=2.4kmになります。
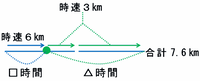
この場合、山道2.4kmを進むのにかかる時間は2.4÷2=1.2時間=1時間12分なので、残りの10-2.4=7.6kmを、2時間10分-1時間12分=58分かけて進むことになります(次の図)。
上の図の□時間を求めるために、「58分すべて時速3kmで進んだら」と仮定して、次の図のようにつるかめ算を行ってみると・・・

つるかめ算をやったら、時速6kmで進んだ(速さを変える前の)平地は9.4kmになりました。
上の図の□時間を求めるために、「1時間34分すべて時速3kmで進んだら」と仮定して、また次の図のようにつるかめ算を行ってみると・・・

ただし、実際には平地Bで速さを変えた地点の前に山道が2.4kmあるので、出発地点から速さを変えた地点までのきょりは、5.8+2.4=8.2kmになります。
(画像はすべて、クリックすると拡大します)
平地Aと平地Bそれぞれの長さは分かっていないのですが、どちらも同じ速度で進むので、大まかにいえばこの徒歩コースは「時速6kmで進む平地」と「時速4kmで進む山道」の2つに分けられます。
2種類のものが混ざっていて、合計のきょり(10km)も分かっているのだから、つるかめ算が使えそうです。
これは山道の長さを求める問題なので、「1時間52分すべてを時速6kmで進んだら」と仮定して、次の図のようにつるかめ算を行います。
※ 計算の中に分数が多く出てくるので、画像に変換します。
つまり、山道を進むのに時速4kmで0.6時間かかるので、4×0.6=2.4kmになります。
(2)
問題文の「最初(1)の速さで進み、ある地点からその後ずっと速さを(1)の半分にして進む」という部分には、2つの意味が込められています。
【速さを平地Aの途中で変える場合】
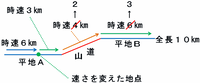
次の図のように、平地Aは途中から時速3km、山道はすべて時速2km、平地Bはすべて時速3kmになります。
この場合、山道2.4kmを進むのにかかる時間は2.4÷2=1.2時間=1時間12分なので、残りの10-2.4=7.6kmを、2時間10分-1時間12分=58分かけて進むことになります(次の図)。
上の図の□時間を求めるために、「58分すべて時速3kmで進んだら」と仮定して、次の図のようにつるかめ算を行ってみると・・・
つるかめ算をやったら、時速6kmで進んだ(速さを変える前の)平地は9.4kmになりました。
でも、この答えは明らかにおかしいですよね。だって、平地の合計は7.6kmしかないんですから(笑)
なぜ答えがおかしくなるのか?それはたぶん、速さを変えた地点が平地Aではなく平地Bの途中にあるからだろうと予想できます。
【速さを平地Bの途中で変える場合】
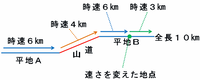
次の図のように、平地Aはすべて時速6km、山道はすべて時速4km、平地Bは途中から時速3kmになります。
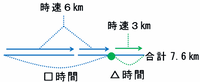
この場合、山道2.4kmを進むのにかかる時間は2.4÷4=0.6時間=36分なので、残りの10-2.4=7.6kmを、2時間10分-36分=1時間34分かけて進むことになります(次の図)。
上の図の□時間を求めるために、「1時間34分すべて時速3kmで進んだら」と仮定して、また次の図のようにつるかめ算を行ってみると・・・
ただし、実際には平地Bで速さを変えた地点の前に山道が2.4kmあるので、出発地点から速さを変えた地点までのきょりは、5.8+2.4=8.2kmになります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
