あきこさんのクラスは滝を見学に行きました。Ａ地点から滝までは道幅がせまいので、３つのグループに分かれて歩くことにしました。グループは①、②、③で、この順に出発しました。
Ａ地点から滝までは４３０ｍあります。どのグループも滝で５分間の休憩をとり、Ａ地点から滝までの道のりを、行きは時速２.４㎞、帰りは時速３㎞の速さで往復しました。グループどうしの間は１０分間あけて出発しました。ただし、グループの列の長さは考えないものとします。次の問いに答えなさい。
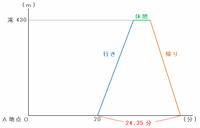
下のグラフは、「グループ①がＡ地点を出発してからの時間」と「それぞれのグループのＡ地点からの距離」の関係を表したものです。
※ 画像はクリックすると拡大します。
(１) グループ③がＡ地点に戻ってきたのは、グループ①がＡ地点を出発してから何分何秒後でしたか。
(２) グラフのアにあてはまる数を求めなさい。
(３) グラフのイにあてはまる数を求めなさい。
(４) グループ③がグループ②とすれちがったのは、Ａ地点から何ｍ進んだところでしたか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは行きと帰りの速さをそれぞれ分速□ｍの形に直しておくと、
・行き→２.４×１０００÷６０＝分速４０ｍ
・帰り→３×１０００÷６０＝分速５０ｍ
となります。
次の図のように、３つのグループは、Ａ地点から滝まで進むのに４３０÷４０＝１０.７５分、そして滝からＡ地点まで戻るのに４３０÷５０＝８.６分かかるので、途中の休憩時間である５分も含めると、往復にかかる時間は１０.７５＋５＋８.６＝２４.３５分になります。
※ 画像はすべて、クリックすると拡大します。
次の図のように、グループ③はグループ①がＡ地点をスタートしてから２０分後に出発し、それから２４.３５分後にＡ地点へ帰ってきます。
したがって、グループ③がＡ地点へ帰ってくるのは、グループ①がＡ地点を出発してから２０＋２４.３５＝４４.３５分＝４４分２１秒後になります。
(２)
次のグラフのアは、滝に到着したグループ①がそこで５分間休憩し、帰りのときの速さで２０－(１０.７５＋５)＝４.２５分引き返したときを表しています。
帰りのときの速さは分速５０ｍなので、グループ①は４.２５分間で５０×４.２５＝２１２.５ｍ進みます。
ただし、それは滝からアまでの距離なので、グラフのア(Ａ地点からアまでの距離)にあてはまる数は、４３０－２１２.５＝２１７.５になります。
(３)
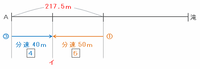
次のグラフのイには、滝へ向かっているグループ③が、滝から戻る途中のグループ①と出会うまでに進んだ距離があてはまります。
グループ③がＡ地点を出発したのは、グループ①がＡ地点を出発してから２０分後なので、その時点でこの２つのグループの間は２１７.５ｍ離れています。
次の図のように、グループ③は滝へ向かって分速４０ｍで、グループ①はＡ地点へ向かって分速５０ｍで進んでいるので、この２つのグループが出会うまでに進む距離の比は、グループ③：グループ①＝分速４０ｍ：分速５０ｍ＝４：５になります。
※ 速さの比＝同じ時間に進む距離の比
上の図でグループ③がグループ①と出会うまでに進んだ距離は２１７.５×９分の４＝３分の２９０ｍなので、グラフのイには３分の２９０があてはまります。
(４)
次のグラフを見れば分かるように、グループ③が②とすれちがう地点ウは、グループ②が①とすれちがう地点エと同じ場所なので、なんとなく計算しやすそうなエの地点がＡから何ｍ離れているのかを求めてみます。
グループ①が滝で休憩を終えてＡ地点へ引き返し始めるのは、Ａ地点を出発してから１０.７５＋５＝１５.７５分後です。
グループ②がＡ地点をスタートするのは、グループ①がＡ地点を出発してから１０分後なので、グループ①が滝から引き返し始めるまでに１５.７５－１０＝５.７５分の余裕があります。
つまり次のグラフのように、グループ①が滝から引き返し始めるまでの５.７５分で、グループ②はＡ地点から４０×５.７５＝２３０ｍ進むことができます。
グループ①が滝から引き返し始めるとき、グループ②は次の図のようにＡ地点から２３０ｍ進んでいるので、２つのグループの距離は４３０－２３０＝２００ｍ離れています。
グループ②とグループ①が進む速さの比は４：５なので、下の図で２つのグループが出会うまでに、グループ②が進んだ距離は２００×９分の４＝９分の８００ｍです。
以上から、グループ②がグループ①とすれちがったのは、Ａ地点から２３０＋９分の８００＝９分の２８７０ｍ進んだ場所になります。
PR
