３匹のヤギがいて、名前はどれも「がらがらどん」です。ですから、Ａ、Ｂ、Ｃと区別することにします。さて、Ａ、Ｂ、Ｃは湖畔の同じ地点を同時に出発し、湖に沿って散歩をしました。Ａは時計回りに、ＢとＣは反時計回りにそれぞれ一定の速さで歩き、Ａの速さはＢの速さの２分の１倍、Ｃの速さはＢの速さの８分の３倍でした。ＡはまずＢと出会い、そこから１２０ｍ歩いた地点でＣと出会い、さらにその２分後に再びＢと出会いました。次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１) 湖は１周何ｍですか。
(２) Ａの速さは毎分何ｍですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
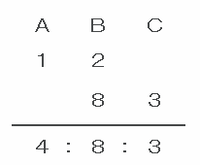
まずはＡとＢ、ＢとＣの速さの比をそれぞれ求めてみると、
・Ａの速さはＢの速さの２分の１倍なので、Ａ：Ｂ＝２分の１：１＝１：２
・Ｃの速さはＢの速さの８分の３倍なので、Ｂ：Ｃ＝１：８分の３＝８：３
となります。
その２つの比を、次の図のように連比にしてみると、３匹の速さの比はＡ：Ｂ：Ｃ＝４：８：３と表せます。
※ 画像はすべて、クリックすると拡大します。
３匹のヤギは、次の図のように点アから同時に出発し、時計回りに進んだＡと反時計回りに進んだＢがコースの途中にある点イで出会いました。
ＡとＢの速さの比は４：８なので、下の図でＡが進んだ距離は４、Ｂが進んだ距離は８、そして湖の１周の距離は４＋８＝１２となります。
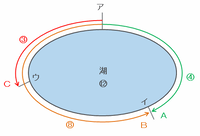
上の図でＡとＢが出会うまでに、Ｃは点アからウまで比の３の距離だけ進んだので、この時点でＡとＣは比の８－３＝５だけ離れていることが分かります。
また、ＡとＣの速さの比は４：３なので、ＡとＣが次の図のように点エで出会うまでに進んだ距離は、
・Ａ→５×７分の４＝７分の２０
・Ｃ→５×７分の３＝７分の１５
と表せます。
上の図で、Ａはイからエまで１２０ｍ進んだので、比の１は１２０÷７分の２０＝４２ｍであることが分かります。
湖の１周の長さは比の１２なので、答えは４２×１２＝５０４ｍになります。
(２)
ＡがＣと出会うまでに点イからエへと進む間、Ｂは反時計回りでイからオへ進みました。
ＡとＢの速さの比は１：２なので、イからエまでの距離が１２０ｍなら、イからオまでの距離は１２０×２＝２４０ｍになります。
湖の１周は５０４ｍ、イからエまでは１２０ｍ、イからオまでは２４０ｍなので、上の図のエとオの間は５０４－(１２０＋２４０)＝１４４ｍ離れています。
その距離を、ＡとＢは１：２の速さで次の図のように２分間進んだら点カで出会ったので、Ａが２分間で進んだエからカまでの距離は、１４４×３分の１＝４８ｍです。
つまり、Ａは２分間で４８ｍ進むので、答えは４８÷２＝分速２４ｍです。
【補足】
問題文に出てくる「がらがらどん」の元ネタは、ノルウェーの童話「３匹のヤギのがらがらどん」です。
３匹のヤギ「がらがらどん」が橋を渡ろうとしたら、その下には怪物がいて・・・というお話なのですが、わりと面白いのでまだ読んだことがない人にはおススメです。
PR
