４つの地点Ａ、Ｂ、Ｃ、Ｄが１０㎞おきにこの順で並んでいます。車①はＡ地点からＤ地点に、車②と③はＤ地点からＡ地点に向かいます。車①、②、③の速さはそれぞれ時速４０㎞、５０㎞、６０㎞です。Ｂ地点とＣ地点の間は車がすれ違うことができないので、対向車がＢ地点とＣ地点の間にいるとき、車①はＢ地点で、車②、③はＣ地点で待たなければなりません。
車②は９時ちょうどに、車③は９時１５分にそれぞれＤ地点を出発します。車の長さは考えず、走っているときは常に一定の速さで走るものとします。
(１)
９時ちょうどに車①がＡ地点を出発すると、車③がＡ地点に着くのは何時何分ですか。
(２)
車①がＢ地点で待つことなく走るには、９時何分と何分の間にＡ地点を出発すればよいですか。ただし、９時から９時３０分の間の時間で考えなさい。
(３)
車②と③が同時にＡ地点に到着するには、車①は何時何分にＡ地点を出発すればよいですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずはそれぞれの車が１区間(１０㎞)を進むのにかかる時間を確認しておきます。
・車①→１０÷４０＝４分の１時間 ６０×４分の１＝１５分
・車②→１０÷５０＝５分の１時間 ６０×５分の１＝１２分
・車③→１０÷６０＝６分の１時間 ６０×６分の１＝１０分
９時ちょうどに車①はＡから、車②はＤからそれぞれ出発します。
車①がＢに着くのは９時１５分、車②がＣに着くのは９時１２分なので、先にＢＣ間を通る権利は車②にあります。
車②がＢに着くのは９時１２分＋１２分＝９時２４分なので、車①は次の図のようにそれまでＢで待つことになります。
※ 画像はすべて、クリックすると拡大します。
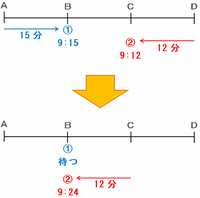
９時１５分にＤを出発した車③がＣに着くのは、９時１５分＋１０分＝９時２５分です。
そのとき、９時２４分までＢで待機していた車①がＢＣ間を通過中なので、今度は車③が次の図のようにＣでしばらく待つことになります。
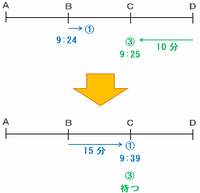
車①がＣに着くのは９時２４分＋１５分＝９時３９分です。
その後は車③がＣからＡまでの２区間を次の図のようにノンストップで進めるので、車③がＡに着くのは９時３９分＋１０分×２＝９時５９分になります。
(２)
車①がＢで待たされることなく走るための条件は、次の３通りが考えられます。
【条件１ 車②がＣに着く前に車①がＢに着く】
車②がＣに着く前に車①がＢに着いてしまえば、Ｂで止まることなく進むことができます。
車②がＣに着くのは９時１２分なので、次の図のように車①もＢへ同じ時刻に着いたとすると、車①はＡを９時１２分－１５分＝８時５７分に出発することになります。
ただし、それだと問題文の「９時から９時３０分までの間」という範囲にあてはまっていないので、答えとしては不適切です。
【条件２ 車②がＢに着くのと同時に車①がＢに着く】
車②がＢに着くのは９時２４分、そして車③がＢに着くのは９時２５分なので、次の図のように車①が９時２４分にＢへ到着すれば、そのままＢＤ間をノンストップで進めます。
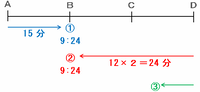
そのとき、車①がＡを出発する時刻は９時２４分－１５分＝９時９分になります。
【条件３ 車③がＣに着く前に車①がＢに着く】
車③がＣに着くのは９時２５分なので、次の図のように車①がそれより前にＢへ到着すれば、そのままＢＤ間をノンストップで進めます。
このとき、車①がＡを出発する時刻は９時２５分－１５分＝９時１０分になります。
以上から、車①がＢで待つことなく走るためには、Ａを９時９分から９時１０分の間に出発することになります。
(３)
ＣからＡまでの２区間を進むのにかかる時間は、車②だと１２×２＝２４分、そして車③は１０×２＝２０分です。
したがって、次の図のように車②が車③よりも２４－２０＝４分早くＣを出発すれば、この２台は同時にＡへ着きます。
また、車③がＣに着く時刻は９時２５分なので、車②はそれよりも４分早い９時２１分にＣを出発することになります。
車②をＣで９時２１分まで待たせるためには、次の図のように車①が先にＢへ到着し、Ｃを９時２１分に通過すればＯＫです。
つまり、車①は９時２１分の３０分前にＡを出発することになるので、答えは９時２１分－３０分＝８時５１分になります。
PR
