気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
11/16
Tue
2010
白百合学園2010【1】 ☆速さ・旅人算☆
列車Aは午後1時に海駅を出ました。列車Aより早く海駅を出た列車Bは午後1時15分に反対方向から来た列車Cに出会いました。その5分後、列車Aも列車Cに出会いました。列車Aと列車Bは午後2時30分に同時に山駅に到着しました。ただし、列車Aの時速は100㎞で、列車Cの時速は80㎞です。
(1) 午後1時15分のとき、列車Aと列車Bの間は何㎞ありますか。
(2) 列車Bの時速を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
(1)
次の図1のように、列車BとCは海駅と山駅の間のどこかで午後1時15分に出会いました。
※ 画像はすべて、クリックすると拡大します。
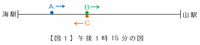
その5分後、今度は列車AとCが次の図2のように出会いました。
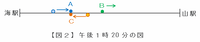
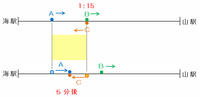
図1と図2を下のように並べてみると、午後1時15分のときの列車AとBの距離の差は、列車AとCが5分間に進んだ距離の合計と等しいことが分かります。
その5分後、今度は列車AとCが次の図2のように出会いました。
図1と図2を下のように並べてみると、午後1時15分のときの列車AとBの距離の差は、列車AとCが5分間に進んだ距離の合計と等しいことが分かります。
5分間は12分の1時間、列車Aは時速100㎞、そして列車Cの時速は時速80㎞なので、AとCが5分間で進む距離の合計は、(100+80)×12分の1=15㎞になります。
(2)
次の図のように、午後1時15分のときには列車AとBは15㎞離れていましたが、午後2時30分にはその差がちょうどなくなり、2つの列車は山駅に到着しました。
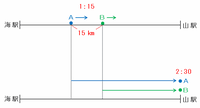
つまり、午後1時15分から午後2時30分までの1時間15分=4分の5時間で15㎞の差が縮まったので、2つの列車の速さの差は15÷4分の5=時速12㎞であることが分かります。
列車Aは時速100㎞なので、列車Bの速さは100-12=時速88㎞になります。
【補足】
列車Bの速さを時速□㎞とおき、「2人の距離の差÷速さの差=追いつくまでにかかる時間」という旅人算の公式を利用して解くと、
15÷(100-□)=4分の5時間
15÷4分の5=12
100-□=12なので、□は100-12=時速88㎞
という感じになります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
