ある時刻に自宅から日光に向けてオートバイで出かけます。時速３０㎞で行くと１０時に目的地に着き、時速５０㎞で行くと８時に目的地に着きます。９時に目的地に着くためには時速( )㎞で行けばよいです。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
距離は「速さ×時間」、長方形の面積は「たて×横」を計算すれば求められるので、時速３０㎞で１０時まで進んだときと、時速５０㎞で８時まで進んだときの距離は、それぞれ次のような長方形に表すことができます。
※ 画像はすべて、クリックすると拡大します。
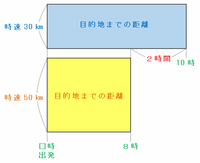
この２つの長方形は、どちらも自宅から目的地までの距離を表しているので面積は同じです。
したがって、この２つの長方形を次の図のように重ねてみると、図の「ア＋イ」と「ア＋ウ」の面積が等しくなるので、イとウの面積は同じであることが分かります。
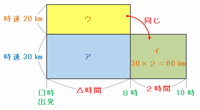
上の図のイは時速３０㎞で２時間進んだときの距離を表しているので、３０×２＝６０㎞です。
また、ウの面積もイと同じく６０㎞なので、上の図の△時間には６０÷２０＝３時間があてはまります。
※ ウの面積→時速２０㎞×△時間＝６０㎞だから。
つまり、自宅から目的地まで時速５０㎞で進むと３時間かかるので、その距離は５０×３＝１５０㎞です。
また、自宅を出発したのは８－３＝５時であることも分かります。
自宅から目的地までの１５０㎞を、５時から９時までの４時間で行くには、１５０÷４＝時速３７.５㎞で進めばＯＫです。
PR
