ある学校の生徒６０人に、犬についてのアンケートをとったところ、「好き」が３２人、「きらい」が１８人、「好きでもきらいでもない」が１０人でした。同じ生徒に、ねこについてのアンケートもとったところ、「好き」が３０人、「きらい」が２１人、「好きでもきらいでもない」が９人でした。また、この２回のアンケートで最低１回は「好きでもきらいでもない」と答えた生徒は１５人でした。
(１)
両方とも「好きでもきらいでもない」と答えた生徒は何人ですか。
(２)
一方に「好き」、他方に「きらい」と答えた生徒は２２人でした。また、一方に「好き」、他方に「好きでもきらいでもない」と答えた生徒は８人でした。
① 両方とも「好き」と答えた生徒は何人ですか。
② 両方とも「きらい」と答えた生徒は何人ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
２回のアンケートで「好きでもきらいでもない」と答えた生徒は１５人なので、もしその１５人全員が「好きでもきらいでもない」と１回しか答えてないのなら、犬とねこを「好きでもきらいでもない」と答えた人の合計も１５人になっているはずです。
しかし実際には、犬とねこを「好きでもきらいでもない」と答えた人の合計は１０＋９＝１９人なので、両方とも「好きでもきらいでもない」と答えた人は１９－１５＝４人だったことが分かります。
【補足】
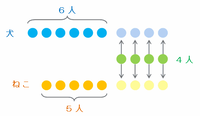
次の図を使って、最低１回は「好きでもきらいでもない」と答えた１５人の内訳を確かめておくと、緑色の４人は犬とねこのどちらも「好きでもきらいでもない」と答えたので、
・犬だけ「好きでもきらいでもない」と答えた人→１０－４＝６人
・ねこだけ「好きでもきらいでもない」と答えた人→９－４＝５人
であることが分かります。
※ 画像はすべて、クリックすると拡大します。
(２)の①
どちらのアンケートも「好き」と「きらい」だけでなく「好きでもきらいでもない」と答えることができるので、この２つのアンケートに対する答え方としては、
Ａ 両方とも「好き」と答える
Ｂ 両方とも「きらい」と答える
Ｃ 両方とも「好きでもきらいでもない」と答える→４人
Ｄ 一方は「好き」、他方は「きらい」と答える→２２人
Ｅ 一方は「好き」、他方は「好きでもきらいでもない」と答える→８人
Ｆ 一方は「きらい」、他方は「好きでもきらいでもない」と答える
の６パターンが考えられます。
この中でＣとＥとＦの合計(最低１回は「好きでもきらいでもない」と答えた人)は１５人なので、ＡとＢとＤの合計(１回も「好きでもきらいでもない」と答えなかった人)は６０－１５＝４５人になります。
また、Ｃは４人なのでＥとＦの合計は１５－４＝１１人、そしてＥは８人なのでＦは１１－８＝３人であることも分かります。
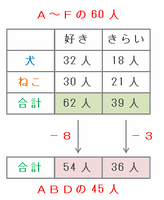
Ａ～Ｆの６０人の場合、犬を「好き」と答えた人は３２人、ねこを「好き」と答えた人は３０人なので、最低１回以上「好き」と答えた人の合計は３２＋３０＝６２人でした。
また、犬を「きらい」と答えた人は１８人、ねこを「きらい」と答えた人は２１人なので、最低１回以上「きらい」と答えた人の合計は１８＋２１＝３９人でした。
その６２人や３９人の中には、Ｅの８人やＦの３人が含まれているのでそれらを除くと、
・最低１回以上「好き」と答えた人→６２－８＝５４人
・最低１回以上「きらい」と答えた人→３９－３＝３６人
となります(次の図参照)。
※ つまり、アンケートで最低１回以上「好きでもきらいでもない」と答えた１５人を除いた４５人を対象とすると、最低１回以上「好き」と答えたのが５４人、最低１回以上「きらい」と答えたのは３６人。
なんで面倒くさい作業をしてそんな数を求めたのかというと、犬とねこのアンケート結果を「好き」と「きらい」の二択でベン図に表すことはできるけど、「好きでもきらいでもない」が混ざるとうまくベン図に表せないから。
これまでに分かったことをもとにして、ＡＢＤの４５人(一度も「好きでもきらいでもない」と答えなかった人)を対象にしたアンケート結果を次のようなベン図に表してみると、
・一度も「好きでもきらいでもない」と答えなかった４５人→図のア＋イ＋ウ＋エ
・一方は「好き」、他方は「きらい」と答えた２２人→図のア＋ウ
・最低１回以上「好き」と答えた５４人→図のア＋イ＋イ＋ウ
となります。
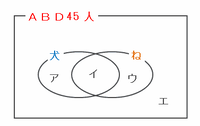
ア＋イ＋イ＋ウ＝５４人、ア＋ウ＝２２人なので、イ＋イ(両方好きな人の数の２倍)は５４－２２＝３２人です。
両方とも「好き」と答えた人数は上のベン図のイにあてはまるので、答えは３２÷２＝１６人になります。
(２)の②
上の図のア＋イ＋ウ＋エ＝４５人、ア＋ウ＝２２人なので、イ＋エ(両方好きまたは両方きらいな人の合計)は４５－２２＝２３人です。
イは１６人なので、エ(両方きらいな人)の数は２３－１６＝７人です。
【補足】
たとえば、上のベン図のエは「両方きらい」を表しているので、「両方好きでもきらいでもない」という人をあてはめることはできません。
また、アは「犬は好きだけどねこはきらい」を表すので、「犬は好きだけどねこは好きでもきらいでもない」という人をあてはめることはできません。
つまりこの問題のように、「好き」と「きらい」以外に「好きでもきらいでもない」という選択肢があると、そのアンケート結果をうまくベン図に表すことができないのです。
そこで、アンケートに答えた６０人ではなく、「好きでもきらいでもない」と答えた１５人を除いたベン図を作成するため、いろいろとややここしい下準備をする必要がありました。
PR
