ある小学校の６年生全員のうち、国語が好きな人は全体の５分の３、算数が好きな人は全体の４分の１、両方とも好きな人は１８人、両方ともきらいな人は４２人でした。６年生全体の人数は( )人です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
次の図のように、６年生全体の人数を１とおいてベン図に表してみると、
・国語が好き(図のア＋イ)→６年生全体の５分の３＝２０分の１２
・算数が好き(図のイ＋ウ)→６年生全体の４分の１＝２０分の５
なので、ア＋イ＋イ＋ウは全体の２０分の１２＋２０分の５＝２０分の１７になります。
※ 画像はすべて、クリックすると拡大します。
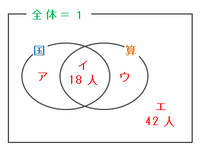
また、ア＋イ＋ウ＋エ＝１なので、次の図のようにさっき作った「ア＋イ＋イ＋ウ＝２０分の１７」という式と並べてみると、
・ア＋イ＋ウ＋エ＝１→イ＋エ＝１８＋４２＝６０人なので、ア＋ウ＋６０人＝１
・ア＋イ＋イ＋ウ＝２０分の１７→イが２つで１８×２＝３６人なので、ア＋ウ＋３６人＝２０分の１７
のようにそれぞれ書き換えることができます。
「ア＋ウ＋６０人＝１」と「ア＋ウ＋３６人＝２０分の１７」にはどちらも「ア＋ウ」が含まれているので、６０－３６＝２４人が６年生全体の１－２０分の１７＝２０分の３にあたることが分かります(次の図参照)。
※ 消去算っぽく式全体を引き算してます。
以上から、６年生全体の人数は２４÷２０分の３＝１６０人になります。
PR
