気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
07/29
Fri
2011
つるかめ算ゆるゆる講座パート1 ☆つるかめ算の仕組みと公式の使い方☆
次の問題を解きながら、つるかめ算の仕組みをサクッと確認してみましょう。
恵里さんがスーパーで1本70円のニンジンと1本90円のゴーヤを合わせて12本買ったら920円でした。このとき、恵里さんはゴーヤを何本買いましたか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
つるかめ算のコツは、最初に「わざと逆方向へ、しかも極端に間違える」ところにあります。
この問題の場合、スーパーで買ったゴーヤの本数を求めたいのですが、あえて「恵里さんは買ったのは全部ニンジン。ゴーヤなんて1本も買ってないよ!」と仮定してつるかめ算をスタートします。
次の図のように、もし恵里さんが買った12本すべてがニンジンなら、合計金額は70×12=840円になります。
しかし、それだと実際の合計である920円に比べて920-840=80円足りません。
※ 画像はすべて、クリックすると拡大します。
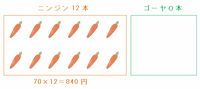
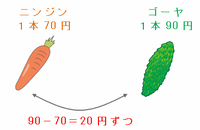
次の図のように、ニンジンとゴーヤの値段を比べてみると、1本当たりの価格差は90-70=20円なので、
・ニンジン1本をゴーヤ1本と交換する→合計は20円高くなる
・ゴーヤ1本をニンジン1本と交換する→合計は20円安くなる
ことが分かります。
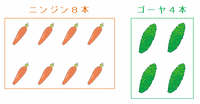
さっき、12本すべてがニンジンだと実際の合計よりも80円足りないことが分かったので、ニンジン1本をゴーヤ1本と80÷20=4回交換すれば実際の合計金額とそろいます。
また、その交換を1回行うごとにニンジンの本数は12本から1本ずつ減り、ゴーヤの本数は0本から1本ずつ増えるので、この問題で求めたいゴーヤの本数は4本、そしてニンジンの本数は12-4=8本になります(次の図参照)。
さて、ここでゴーヤの本数が分かるまでに行った作業を振り返ってみると、
① ニンジン12本の値段は70×12=840円
② 実際の合計よりも920-840=80円少ない
③ ニンジン1本をゴーヤ1本と交換するたびに、合計は90-70=20円ずつ増える
④ その作業を80÷20=4回行えばピッタリ
⑤ もともとゴーヤは0本だったので、ゴーヤの本数は4本
という5つの段階があったのですが、実際に参考書とか問題集の解説を見ると
・(920-70×12)÷(90-70)=4本
・(920-840)÷(90-70)=4本
という形でひとまとめの公式として扱われている場合がほとんどです。
しかし、つるかめ算の公式で求められるのは「ゴーヤの本数」ではなく「ニンジンとゴーヤを何回交換するとピッタリなのか」であり、たまたま①のときに「たぶん12本すべてがニンジン。ゴーヤは0本だよ!」と仮定して計算をスタートしたので、
・ニンジン1本とゴーヤ1本の交換を4回すればOK
・つまり、ゴーヤは4本増える
・もともとゴーヤは0本だったから、交換回数=ゴーヤの本数になってる
という流れになるのです。
したがって、つるかめ算の公式を使って「交換回数=求めたいものの個数」にするためには、最初に「○個すべてがその問題で求めたいものではなく、もう一方の種類のものだったら」と仮定する必要があります。
※ ゴーヤの本数を求めたいなら「もし12本が全部ニンジンだったら」、ニンジンの本数を求めたいなら「もし12本が全部ゴーヤだったら」という感じ。
じゃあ、もしさっきの問題で「たぶん12本すべてがゴーヤだよ。ニンジンなんて1本も買わなかったよ」と仮定してつるかめ算を始めたらどうなるのかというと・・・
① ゴーヤ12本の値段は90×12=1080円
② 実際の合計よりも1080-920=160円多い
③ ゴーヤ1本をニンジン1本と交換するたびに、合計は90-70=20円ずつ減る
④ その作業を160÷20=8回行えばピッタリ
⑤ そのとき、ゴーヤは8本減るので、答えは12-8=4本
という流れで、ちゃんとゴーヤの本数が求められます。
ただしこの場合、「交換回数=ニンジンの本数」なので、最後に「12-8=4本」という計算が必要となり、その分だけ余計な手間がかかります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
