気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
10/01
Fri
2010
浅野2010【7】 ☆規則性・薬師算を読み解く☆
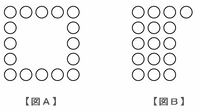
次の図Aのような、一辺が5個の正方形の形に置いた碁石を、図Bのように、たての列の個数がAと同じになるように並べかえます。すると図Bは、たての列が3列と余り1個となります。同じように、一辺が5個以上の正方形の形に置いた碁石を並べかえたときの余りの個数のことを「端数」と呼ぶことにします。図Bの場合は、「端数が1」となるわけです。このとき、次の各問いに答えなさい。それぞれ考え方と計算も書きなさい。
※ 画像はクリックすると拡大します。
(1)
一辺が6個の正方形を並びかえたときの端数を求めなさい。
(2)
端数が4となるときの碁石の総数を求めなさい。
(3)
碁石の総数は、「(端数)×( ア )+( イ )」で求めることができます。この( ア )と( イ )にあてはまる数をそれぞれ求めなさい。
【問題文の追記】
この方法は「薬師算」と呼ばれ、江戸時代に書かれた和算書「塵却記」に載っているものです。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
PR
09/26
Sun
2010
東京農業大学第一2010【5】 ☆規則性・奇数番目と偶数番目の規則を見分ける☆
数字の書かれたブロックが、ある規則に従って次の図のように並べてあります。以下の各問いに答えなさい。
09/15
Wed
2010
早稲田実業2010【4】 ☆規則性・デジタル時計の電気代を求める☆
公園に大きなデジタル時計があります。この時計は0:00から23:59の24時間表示です。15時3分は次の図1のように、6時30分は図2のように表示されます。
※ 画像はすべて、クリックすると拡大します。

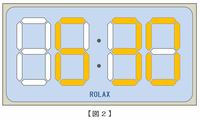
この時計のひとつひとつの数字は、図3の7本のライトに電気がついて表示され、このライト1本を1分間つけるのに必要な電気代は1円です。0から9までの数字の表示方法と1分間の電気代は下の表1の通りです。時と分の間にある2つの点「:」の電気代は考えません。


0:00からの5分間は、0:00が表示されはじめてから0:04の表示が終わるまでとして、次の( )をうめなさい。
0:00からの5分間は、0:00が表示されはじめてから0:04の表示が終わるまでとして、次の( )をうめなさい。
(1) 6:30からの10分間にかかる電気代は( )円です。
(2) ( : )からの10分間にかかる電気代が一番高くなります。
(3) 11:( )からの5分間にかかる電気代は60円です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
09/13
Mon
2010
攻玉社2010【2】 ☆規則性・異なる規則で並んだ2列の碁石☆
次の図は、まこと君とたろう君の2人が、ある規則が繰り返されるような並べ方で白と黒の碁石を並べたものです。図のように、1番目から①、②、③、・・・と番号を付けていくとき、次の問いに答えなさい。
09/05
Sun
2010
早稲田実業2010【3】 ☆規則性・外側に接する円の個数☆
次の図のように円を並べていきます。円の中の数字は、その円と接している円の個数を表しています。次の各問いに答えなさい。
09/01
Wed
2010
立教新座2010【4】 ☆規則性・約数の性質を利用する☆
08/28
Sat
2010
横浜雙葉2010【3】 ☆規則性・約数の性質を利用する☆
偶数2、4、6、8、10、・・・・・を次のルールにしたがって、下の表にならべます。
※ 画像はすべて、クリックすると拡大します。
【ルール】
① 偶数を商が奇数になるまで2で何回も割ります。
② 2で割ることができた回数をX、奇数の商に1を加えて再び2で割った商をYとします。
③ その偶数をX行目のY列目にならべます。
たとえば、20は
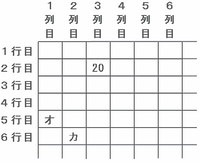
20÷2=10、10÷2=5、(5+1)÷2=3なので、X=2、Y=3ですから、2行目の3列目にならべます。
次のア~シにあてはまる数を求めなさい。
(1) 24はア行目のイ列目にくる数です。
(2) 50はウ行目のエ列目にくる数です。
(3) 5行目の1列目にくる数はオです。
(4) 6行目の2列目にくる数はカです。
(5) キ、ク、ケが次の図のようにならんでいます。クはキよりも16だけ大きくケよりも56だけ小さいです。
08/09
Mon
2010
愛知淑徳2010【7】 ☆規則性・対戦相手が入れ替わる☆
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
