気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
06/03
Thu
2010
春日部共栄2010【4】 ☆場合の数・道の通り方を数える☆
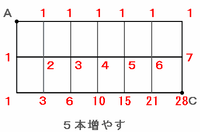
図のように道で分けられた2つの土地があります。このとき、AからCへ遠回りしないで行く行き方は、A→E→B→C、A→D→F→C、A→E→F→Cの3通りです。
※ 画像はすべて、クリックすると拡大します。

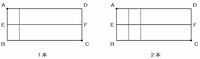
(1) たての道を5本増やしたとき、AからCへの行き方は全部で( )通りあります。
※ 画像はすべて、クリックすると拡大します。
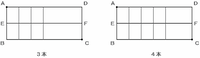
この土地にたての道を1本ずつ増やし、土地を分けることを考えます。次の( )に適当な数を入れなさい。
(1) たての道を5本増やしたとき、AからCへの行き方は全部で( )通りあります。
(2) たての道を( )本増やしたとき、AからCへの行き方は全部で1540通りあります。
(3) 道で分けられた土地の数が210となったとき、AからCへの行き方は全部で( )通りあります。
※ 解説を見る場合は、下の「解説はこちらから」をクリック!
(1)
たての道を5本増やしたときの行き方だけ数えてもOKなのですが、次の問題に向けて規則性を確認しておく必要がありそうなので、まずはたての道を1本から4本増やしたときそれぞれの場合行き方が何通りなのかを数えてみます。
「下の赤い数字の意味がよく分からん」という場合、まずはコチラの説明を簡単に読み流してみてください。
※ 画像はすべて、クリックすると拡大します。
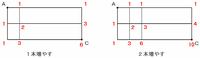
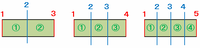
上の図を見て、たての道の本数と行き方の数との関係にピンと来ましたか?
でもこの時点で規則性に気がついていなくても、5本程度なら次のように図で確認すればOKです。
上の図から、たての道を5本増やしたときの行き方は全部で28通りになります。
(2)
たての道をどんどん増やして1540通りになるときを見つけるのはどう考えても大変そうなので、さっき確認したことを利用して「たての道の本数と行き方の数との規則性」を見つけてみます。
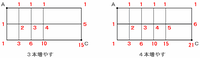
・たての道を1本増やす→たての道は両側もふくめて全部で3本→行き方は6通り
・たての道を2本増やす→たての道は両側もふくめて全部で4本→行き方は10通り
・たての道を3本増やす→たての道は両側もふくめて全部で5本→行き方は15通り
・たての道を4本増やす→たての道は両側もふくめて全部で6本→行き方は21通り
・たての道を5本増やす→たての道は両側もふくめて全部で7本→行き方は28通り
たとえばたての道が両側もふくめて3本あるとき、行き方は全部で1+2+3=6通りになっています。
両側もふくめて4本のときは1+2+3+4=10通り、5本のときは1+2+3+4+5=15通りになっていることからも分かるように、たての道が両側もふくめて□本あるとき、行き方は1から□までの数列の和と同じだけあります。
したがって、行き方が1540通りになるときの両側を含めたたての道の本数を□本とおくと、(1+□)×□÷2=1540という式に表せます。
このとき、(1+□)×□の答えが1540×2=3080なので、1ちがいの2つの数をかけ合わせて3080になる場合を探してみます。
※ 「5×6」とか「8×9」とか。見つけるのはそんなに難しくないです。
まず、ものすごく大ざっぱに言って、3080は「50×50=2500」と「60×60=3600」の間にあるので、1ちがいの2つの数の十の位には、どちらも「5」があてはまります。
それと、答えの一の位が「0」なので、1ちがいの一方の数には一の位に「0」または「5」があるはずです。
ただ、50×51は明らかに3080より小さいので、「0」ではなく「5」がある場合を考えてみます。
1ちがいの2つの数のどちらかが55の場合、もう一方の数とのかけ算の組み合わせは「54×55」と「55×56」の2通りが考えられます。
このとき、54×55=2970、55×56=3080なので、あてはまるのは「55×56」だと分かります。
つまり、(1+□)×□=3080=56×55になることが分かったので、□には55があてはまります。
ただし、それは最初から両側にあるたての道もふくめた本数なので、増やした本数は55-2=53本になります。
(3)
土地の数が上下2段で210のとき、土地は上段だけに210÷2=105か所あります。
次の図を見れば分かるように、たての道が両側をふくめて3本のときは土地が2か所、4本のときは3か所、そして5本のときは4か所となっていることから、両側をふくめたたての道が□本あるとき、「□-1=上段にある土地の数」という式ができます。
□-1=105のとき、□は105+1=106となります。
つまり、たての道は両側をふくめて106本あるので、行き方は1から106までの和と等しくなります。
以上から、行き方は全部で(1+106)×106÷2=5671通りになります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
